What Comes Next: 1, 2, 4, 8, 16, … hint it’s not 32

A Kick in the Discovery

, , ,

Newbie at Number Theory (Part Two): The Euclidean Algorithm

Published by

Valt

on

Today’s part two of our dive into number theory. For those who haven’t read part one about the division algorithm click here, because we plan to use it! We talk everything Euclidiean, except for Euclidean geometry! We will learn about another algorithm which is a very useful tool to find common divisors of two integers. More than that, it can be used to find all combinations of those integers! But I’m getting ahead of myself. We start at the beginning and discuss the Euclidean Algorithm and the greatest common divisor.

Some Notation

Like any branch of mathematics, there are certain notation conventions that are used. Number theory is no different. We want a shorthand for when a number is a divisor of another number.

For example, 5 is a divisor of 15. Likewise, 24 is a divisor of 96. Another way to say these two facts is: 5 divides 15 and 24 divides 96. The way we write this shorthand is the following:

Notation: Let n and d be integers such that n =dk for some integer k, then we say d divides n . And we write d\mid n . Hence the following two are equivalent statements:

d\mid n \;\;\iff\;\; n = dk.

We can also say n is a multiple of d .

(NOTE: n,d,k are all integers)

With the numbers we were using we’d write:

5 \mid 15 since 15 = 5(3)

and

24 \mid 96 since 96=24(4) .

Since 3 and 4 are integers.

The Greatest Common Divisor

When I was in school, I would always confuse the greatest common divisor and the least common multiple. Both are important (and related to one another), but we will focus on the greatest common divisor today.1

If you remember from school, the greatest common divisor of integers n and m is the largest number that divides both n and m . For example, the greatest common divisor of 30 and 42 is equal to 6, since (i) both 30 and 42 are divisible by 6 and (ii) no number larger than 6 divides 30 and 42.

In elementary school the way I found the greatest common divisors was by listing the divisors of each number and finding the integers common to both lists. Using 30 and 42 again, I would have done the following:

30\;\;:\;\; \boxed{1}\;,\;\boxed{2}\;,\;\boxed{3}\;,\;5,\;\boxed{6}\;,\;10,\;15,\;30

42\;\;:\;\; \boxed{1}\;,\;\boxed{2}\;,\;\boxed{3}\;,\;\boxed{6}\;,\;7,\;14,\;21,\;42

Where the boxed numbers are the ones that are common between the two lists. Then I’d search for the greatest common number on the lists. In this case, it was 6. Thus, the greatest common divisor of 30 and 42 is equal to 6. Not bad…

This method is surefire; however, it’s not the best thing we can do. For example, if I gave you the numbers 1,231,872,638,162 and 9,287,391,721,397. How would you write out the factor lists? You’d need to know the prime factorization of both numbers to even start. Not good.

This is where the Euclidean Algorithm comes into play. It’s a set of steps that allow us to find the greatest common divisor of two numbers without needing to do any factorization. However, it can require a lot of steps and sometimes it would be easier to just factor, so it’s not perfect. For example, if all I needed was the greatest common divisor of 30 and 42, I would not use the Euclidean Algorithm, because factoring 30 and 42 is easy. But for numbers like 1,231,872,638,162 and 9,287,391,721,397, I would use Euclidean Algorithm because factoring these numbers is much harder to do.

The Euclidean Algorithm also has some other advantages. But let’s leave this for the section Mysterious Motivation.

Before we move on, let’s write out the definition of the greatest common divisor.

Definition: The greatest common divisor d of two integers, a and b is the unique integer that satisfies:

  1. It’s a divisor of both a and b , ie d \mid a and d\mid b , and
  2. For any other common divisor d_2 where both d_2\mid a and d_2\mid b , it must be d_2 \leq d .

If d satisfies both criteria then we write \gcd{(a,b)} = d .

From before, 6\mid 30 and 6\mid 42 . And all the common factors of 30 and 42 are {1, 2, 3, 6}. Note how they are all smaller than or equal to 6.

NOTABLE EXAMPLE: Let us consider when a is a multiple of b ie when a = bk for some integer k. What’s \gcd{(a,b)} = ??? . Well, since (1) by construction b\mid a and since b=b(1) we have b\mid b ; and (2) no number larger than b can divide b (so that b is the largest divisor of b). We conclude \gcd{(a,b)} = b.2 Remember this for later: a = bk implies \gcd{(a,b)} = b.

The Euclidean Algorithm

This algorithm notationally is very confusing, however, actually doing it isn’t so bad once you get the hang of it. The idea is the following:

We have integers a and b with a>b. Goal: find the greatest common divisor of a and b . First, we use the division algorithm to conclude,

a=q_0b+r_0 \;\;\;\mathrm{where}\;\;0\leq r_0<b.

Next, focus on the remainder r_0 . There are two things that can happen, either r_0= 0 or r_0\neq 0 . When r_0= 0 we are done!3 Since this means that a is a multiple of b because a =q_0 b . So we conclude \gcd{(a,b)} = b (remember what I said to remember for later?)! So let us assume that r_0\neq 0 .

Here’s the key: We claim, that if r_0\neq 0 then \gcd{(a,b)} = \gcd{(b,r_0)}.

If that’s true, since a>b>r_0, we can instead work with the smaller integers b and r_0 when finding the greatest common divisor of a and b. This is useful because we might be able to factor b and r_0.

However, sometimes we still cannot factor b and r_0. But don’t fret, since r_0\neq 0 we can play the same game with the division algorithm:

b=q_1r_0+r_1 \;\;\;\mathrm{where}\;\;0\leq r_1<r_0

Like earlier, if r_1 = 0 then b = q_1 r_0 and we would conclude \gcd{(a,b)} = \gcd{(b,r_0)}=r_0 and be done. If we’re not so lucky and r_1 \neq 0, we claim something similar to earlier:

We claim, if r_0\neq 0 then \gcd{(a,b)} = \gcd{(b,r_0)}=\gcd{(r_0,r_1)}.

Like before, a>b>r_0>r_1 so we can begin working with even smaller integers when finding \gcd{(a,b)}!

We might now be able to factor r_0 and r_1 , but who cares! This is too much fun! So, if r_1 \neq 0 let’s do the same thing again . . .

. . . and again, and again, and again, as long as the remainders are nonzero. Let’s not worry if we can factor our new smaller numbers at each step.

We’d end up with something like this:

We’d get some remainder r_{n+2}=0 and finally, be done. Then since all the previous remainders are nonzero, (r_0, r_1, \cdots, r_{n+1}\neq 0) We claim we get the chain:

\gcd{(a,b)} = \gcd{(b,r_0)}=\gcd{(r_0,r_1)}=\cdots =\gcd{(r_n,r_{n+1})}.

with decreasing integers: a>b>r_0>r_1>r_2>\cdots>r_{n+1}>r_{n+2}=0.

Since r_{n+2}=0, we deduce \gcd{(a,b)} = \gcd{(b,r_0)}=\gcd{(r_0,r_1)}=\cdots =\gcd{(r_n,r_{n+1})} = r_{n+1} since r_{n+2}=0 implies r_{n} is a multiple of r_{n+1} just like earlier.

And where done!

But did you notice that we just implicitly assumed that at some point these steps would come to an end when a remainder would equal zero, in this case r_{n+2}=0. But does this ever not happen? No, since all of these remainders are greater than or equal to zero and all of them are strictly smaller than the previous, they form a set of decreasing integers:

a>b>r_0>r_1>r_2>\cdots>r_{n+1}>r_{n+2}\geq 0.

And since there are only finitely many integers less than a but greater than 0 (namely 1,2,3,\cdots,a-1 ) the process must come to an end because some remainder reaches zero.

If every claim made above is true, then we’re done! We have found The greatest common divisor, \gcd{(a,b)} = r_{n+1} without factoring! This is the Euclidean algorithm. We progressively use the division algorithm in order to find smaller and smaller numbers to use to find the greatest common divisor, which ends up being the last nonzero remainder from the division algorithm.

Let’s do an example and then we’ll go through the proof. But, to make the algorithm easier to follow, here is a schematic:

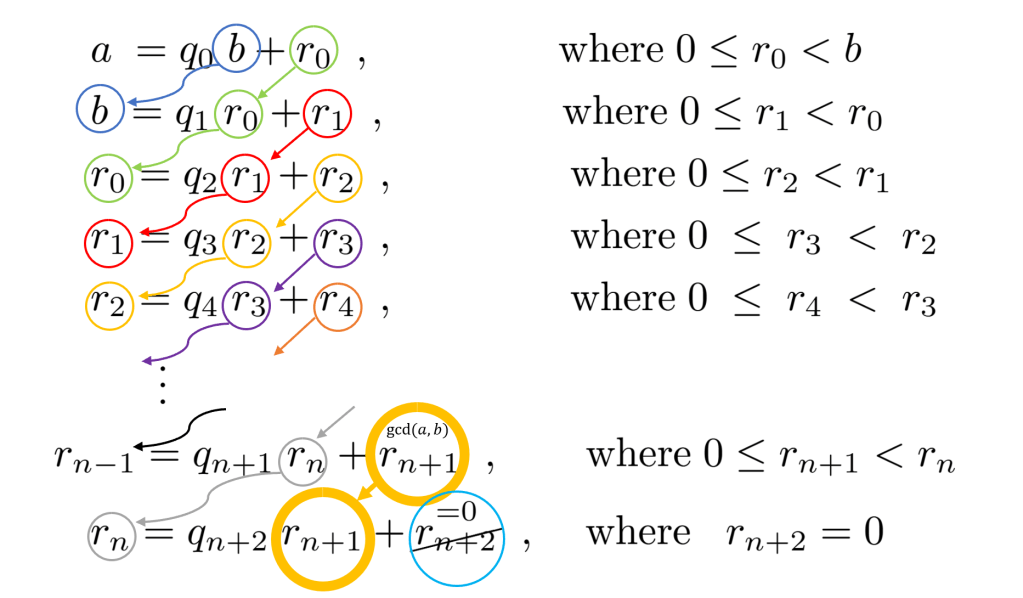
Where you conclude \gcd{(a,b)} = r_{n+1} .

Example 1: gcd( 59 , 301)

Remember, we progressively use the division algorithm, and the last nonzero remainder is the greatest common divisor.

Thus, \gcd{(59,301)} = 1.

Example 2: gcd ( 142 , 262) =2

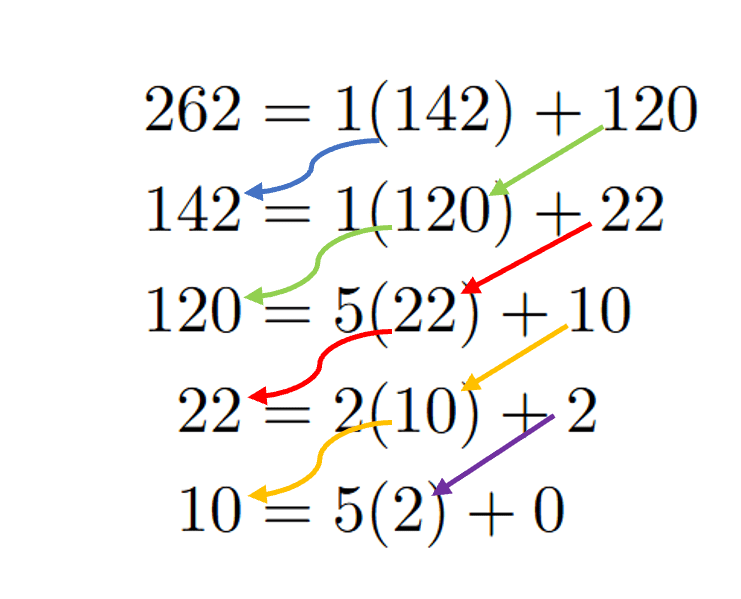
Thus \gcd{(142,262)} = 2.

Euclidean Algorithm “Proof”

Lemma:

Let a and b be positive integers with a> b . If a=q_0b+r_0 \;\;\;\mathrm{where}\;\;0\leq r_0<b, then \gcd{(a,b)} = \gcd{(b,r_0)}.

Proof of Lemma: (Click in the Discovery)

Let a and b be positive integers with a> b . Let’s label \gcd{(a,b)} = d_1 and \gcd{(b,r_0)}=d_2 . Our goal is to show that d_1 =d_2. We’ll accomplish this by showing:

d is divisor of a and b if and only if d is a divisor of b and r_0.

Or, the set of divisors of a and b is the same as the set of divisors of b and r_0.

Why would this imply d_1 =d_2?

We know d_1 is a divisor of both a and b (since it’s their greatest common divisor), and the statement above implies that d_1 also a divisor of b and r_0. But recall that d_2 is the greatest common divisor of b and r_0 and therefore d_1 \leq d_2 by part (2) of the definition of the greatest common divisor. A similar argument shows d_1 \geq d_2 and hence d_1 =d_2.

So, if we can prove the set of divisors of a and b is the same as the set of divisors of b and r_0, then we’re done!

Forward: If d is divisor of a and b then d is a divisor of b and r_0.

Consider some divisor d of a and b. By the definition of a divisor, d \mid a and d\mid b is equivalent to saying a =dk and b=dt for integers k and t .

Recall the division algorithm tells us there exists integers q_0 and r_0 such that:

a=q_0b+r_0 \;\;\;\mathrm{where}\;\;0\leq r_0<b.

Solving for r_0 we get,

r_0=a-q_0b .

Using our knowledge that a =dk and b=dt we conclude,

r_0=a-q_0b = dk - q_0dt = d(k-q_0t).

Hence d is a divisor r_0 since r_0 has the form: d\cdot (INTEGER).

Backwards: If d is divisor of b and r_0 then d is a divisor of a and b.

The proof of the backward direction is the same as the forward direction, for the most part… So, I challenge you to finish this proof!

Conclusion: Since d is divisor of a and b if and only if d is a divisor of b and r_0, it must be that \gcd{(a,b)} = \gcd{(b,r_0)} from the reasoning that we used earlier.

\square

We now have enough to prove the next theorem!

Theorem: The Euclidean Algorithm really works…

Proof Idea: By repeatedly applying the division algorithm we end up with a chain of remainders with the property that each one is less than the previous. Since each remainder is greater than or equal to 0, this chain must come to an end because there are only finitely many integers less than a but greater than 0.

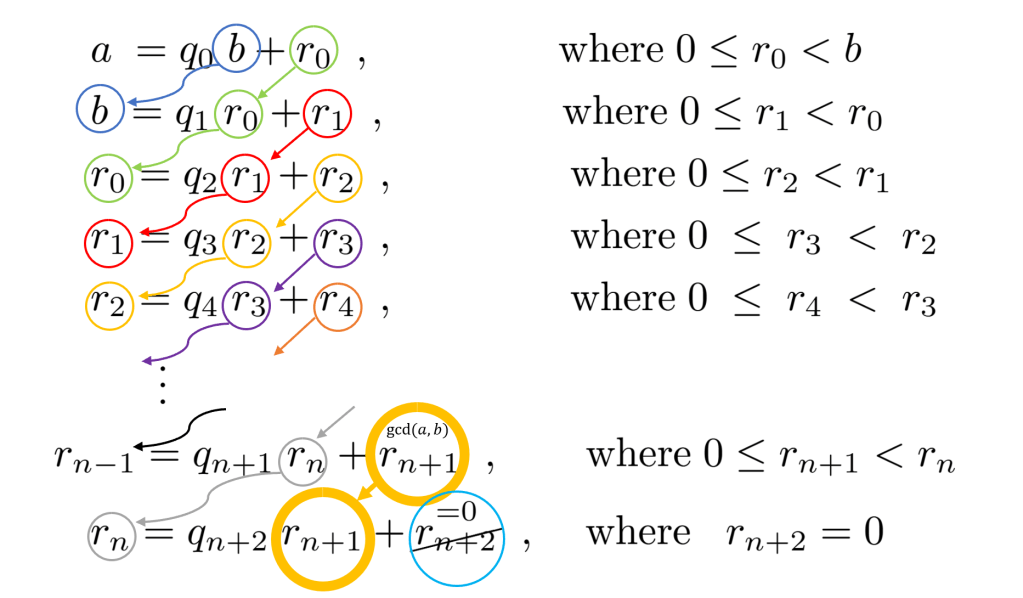
Let’s say r_{n+2} =0. Therefore,

a>b>r_0>r_1>r_2>\cdots>r_{n+1} >r_{n+2}=0.

By applying our lemma at each step, the greatest common divisor is ‘carried along’ each step, meaning:

\gcd{(a,b)} = \gcd{(b,r_0)}=\gcd{(r_0,r_1)}=\cdots =\gcd{(r_n,r_{n+1})} = r_{n+1}.

Where we used that r_{n+2}=0 implies,

r_n=q_{n+2}r_{n+1} \iff r_{n+1}\mid r_n.

Thus, \gcd{(r_n,r_{n+1})} = r_{n+1} as stated.

A Motivating Mystery

Ok, so we have the Euclidean Algorithm now. We know how to use it, is it good for anything? Yes. It can be used to answer the following questions:

Let’s consider,

2x + 4y = 1 .

Are there integer solutions? Meaning are there integers x and y that make this true? (For example x=3 and y =-1 don’t work since they give 2(3) + 4(-1) = 2 \neq 1 ).

Give it a try!

I’ll wait…

Did you find any?

No?

Does that mean you didn’t try enough, or are there no solutions?

Ok, try this one:

2x + 5y = 1 .

It’s almost the same as the first.

Give it a go!

Did you find any?

Maybe x = -2 and y = 1: since 2(-2) + 5(1) = -4 + 5 = 1 . Or maybe you found x=3 and y=-1 since 2(3) + 5(-1) = 6 - 5 = 1 . Or maybe you found another one that wasn’t either of the two above!

The first equation has no solutions whereas the second one has infinitely many solutions.

What’s the problem with the first equation, why are there no solutions? And what’s so nice about the second equation that allows for infinitely many solutions?

Unfortunately, this blog is tooooo long as it is. So, you’ll have to wait until next week! Try to come up with a conjecture of your own. Remember it’s all about a Kick in the Discovery!

TO BE CONTINUED…

Closing Remarks

Though you may think that the Euclidean Algorithm isn’t very useful in an age when you can just ask Wolfram Alpha to find the greatest common divisor of any two integers you want, and you’re partly right since most computations and arithmetic are no longer done by hand (unless you are taking a test and your teacher doesn’t allow calculators, in which case that stinks and I’m sorry!)4 The utility of the Euclidean Algorithm is in its application to theory. As well see next time, it has far-reaching implications.

Footnotes:

  1. Ok, I couldn’t help myself. Let a and b be positive integers, then the connection between the greatest common divisor and least common multiple is ab = \gcd{(a,b)} \cdot \mathrm{lcm}{(a,b)} where \mathrm{lcm}{(a,b)} is the least common multiple. of a and b. ↩︎
  2. For example, \gcd{(36,12)} = 12 or \gcd{(150,30)} = 30. ↩︎
  3. To the person who invented the number 0, thanks for nothing! ↩︎
  4. One mathematician says to the other, “Did you know that only 99.9% of people know some number theory? And luckily, I’m one of the 10% who do!” ↩︎

One response to “Newbie at Number Theory (Part Two): The Euclidean Algorithm”

  1. Newbie Number Theory: (Part 3) ax+by=1 – A Kick in the Discovery Avatar
    Newbie Number Theory: (Part 3) ax+by=1 – A Kick in the Discovery

    […] Last time we left off with a mystery… But before we get to that, a little introduction. […]

    Like

    Reply

Leave a comment