Euler’s Formula as a Tool for Fast Trigonometry

Preamble (Feel free to skip)

There are many times (at least in school) where we need some random trigonometric identity to be able to solve a problem. At least for me, I’ve never bothered to memorize the double angle formula or the sum of angles formulae! I’m guessing most of you are in a similar boat to me. It seems to be a trend that people who enjoy math enjoy it because they can be ~~lazy~~ efficient with what they need to memorize. Also, I’ve been in a few conversations with friends and fellow math enthusiasts where I found out they were unfamiliar with some tricks you can perform using Euler’s formula in regard to deducing trigonometry identities. This cannot stand! It’s too wonderful and simple (compared to the geometry proofs) to derive complicated trigonometry identities using Euler’s formula to not tell you about!

Euler’s Formula

Considered by many to be the most beautiful math equation of all time, I would not be surprised if a few of you have already come across Euler’s formula. But, to make sure we are all up to speed here it is,

$e^{i \theta} = \cos{(\theta)} + i \sin{(\theta)}.$

Deceptively simple, it gives us a remarkably easy way to work with complex numbers. That’s for another day however, today all we need to know is that $i^2 = -1$ , how to work with exponents: $e^{a}\cdot e^{b} = e^{a+b}$ and $e^a/e^b = e^{a-b}$ , and that $a+ib = x+iy$ if any only if $a=x$ and $b=y$ where $a,b,x,y$ are all real numbers. We call the part without $i$ the real part of the complex number and we call the part with $i$ the imaginary part.

For example, $2 + 3i$ is a complex number with real part equal to 2 and imaginary part equal to 3.

Sin(a+b)=? and Cos(a+b)=?

Using Euler’s formula we see,

$e^{i (a+b)} = \cos{(a+b)} + i \sin{(a+b)}.$

But, using our exponent product rules we can also equate the above equation with,

$e^{i (a+b)} = e^{ia} \cdot e^{ib}.$

Why is this useful? Because we can then use Euler’s formula on $e^{ia}$ and $e^{ib}$ to get,

$e^{i (a+b)} = e^{ia} \cdot e^{ib} \\\textit{ }\qquad\; =\Big(\cos{(a)} + i \sin{(a)}\Big)\Big(\cos{(b)} + i \sin{(b)}\Big) .$

Which, by foiling out the product we get,

$e^{i (a+b)} = \cos{(a)}\cos{(b)} + i \cos{(a)}\sin{(b)} + i \sin{(a)}\cos{(b)} + i^2 \sin{(a)} \sin{(b)}\\\textit{ } \; \\\textit{ }\qquad\, = \Big(\cos{(a)}\cos{(b)} -\sin{(a)} \sin{(b)} \Big)+ i \Big( \cos{(a)}\sin{(b)} + \sin{(a)}\cos{(b)} \Big) .$

Where we grouped all the real terms into the first parenthesis and the imaginary terms into the second set of parentheses. Using our very first expression for $e^{i(a+b)}$ we deduce,

$\cos{(a+b)} + i \sin{(a+b)} = \Big(\cos{(a)}\cos{(b)} -\sin{(a)} \sin{(b)} \Big)+\\\textit{ }\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\; i \Big( \cos{(a)}\sin{(b)} + \sin{(a)}\cos{(b)} \Big) .$

Recall that two complex numbers are equal if and only if the real parts are equal:

$\boxed{\cos{(a+b)} = \cos{(a)}\cos{(b)} -\sin{(a)} \sin{(b)} },$

and the imaginary parts are equal:

$\boxed{\sin{(a+b)} = \cos{(a)}\sin{(b)} + \sin{(a)}\cos{(b)} }.$

Just like that we figured out what the sum of angles formula are for sine and cosine! We didn’t even need to draw a single triangle! How amazing is this! Even though I love triangles and geometry, I still find it immensely pleasing that this works at all!

Cos(a)Cos(b)

We are going to use a slightly different strategy. First, consider $e^{-i\theta}.$ Using Euler’s formula (again) we can see,

$e^{- i \theta} = \cos{(-\theta)} + i \sin{(-\theta)}.$

Recalling that $\cos{(-\theta)} = \cos{(\theta)}$ and $\sin{(-\theta)} = -\sin{(\theta)}$ we get the following,

$e^{- i \theta} = \cos{(\theta)} - i \sin{(\theta)}.$

Vocabulary Alert: For some complex number $z=a+ib$ we call $\bar{z}=a-ib$ the complex conjugate of $z$ .¹ We have deduced that,

$e^{\pm i \theta} = \cos{(\theta)} \pm i \sin{(\theta)}.$

Question, what is the sum of $e^{i\theta}$ and $e^{-i\theta}$ ? Using what we just found we see,

$e^{i\theta}+ e^{-i\theta} = \Big(\cos{(\theta)} + i \sin{(\theta)}\Big) + \Big(\cos{(\theta)} - i \sin{(\theta)}\Big)\\\textit{ } \\\textit{ }\qquad\;\;\;\;\;\; = 2\cos{(\theta)}$

How wonderful! Solving for cosine we get,

$\boxed{\cos{(\theta)} = \frac{e^{i\theta}+ e^{-i\theta}}{2}}.$

In some way, we could use this equation to define the cosine function without appealing to any triangles (again!).

Let’s use our newfound expression for cosine to find $\cos{(a)}\cos{(b)}$ .

$\cos{(a)}\cos{(b)} = \Big(\frac{e^{i a}+ e^{-i a}}{2}\Big)\cdot \Big(\frac{e^{i b}+ e^{-ib}}{2}\Big)\\\textit{ }\qquad\qquad\;\;\;\;\; = \frac{1}{4} \Big(e^{i(a+b)} + e^{i(a-b)}+e^{i(-a+b)}+e^{i(-a-b)}\Big).$

With a little rearranging we deduce,

$\cos{(a)}\cos{(b)} = \frac{1}{4} \Big(e^{i(a+b)} + e^{i(a-b)}+e^{-i(a+b)}+e^{-i(a-b)}\Big)\\ \textit{ }\; \\\textit{ }\qquad\qquad\;\;\;\;\; = \frac{1}{2}\Bigg(\Big(\frac{e^{i(a+b)} + e^{-i(a+b)}}{2}\Big) + \Big(\frac{e^{i(a-b)} + e^{-i(a-b)}}{2}\Big)\Bigg)\\ \textit{ }\;\\\textit{ }\qquad\qquad\;\;\;\;\; =\frac{1}{2}\Big(\cos{(a+b)}+\cos{(a-b)}\Big).$

Just like that, we have it! Not too bad huh? This is what I use whenever I need to use some trig identity that I haven’t memorized, yet. It’s fast, and when you get used to it you can skip lots of algebra steps making it quicker!

Just to make sure you can easily find the result if you come back to the article,

$\boxed{\cos{(a)}\cos{(b)} = \frac{1}{2}\Big(\cos{(a+b)}+\cos{(a-b)}\Big)}.$

Sin(a)Sin(b)

You can use the exact same logical steps to deduce the product formula for sine. We just need to find a formula for sine in terms of complex exponentials (like $\cos{(\theta)} = \frac{e^{i\theta}+ e^{-i\theta}}{2}$ for cosine).

We have $z = x+iy$ and $\bar{z} = x-iy$ and we want to solve for the imaginary part of $z$ , since sine is the imaginary part of $e^{i\theta}$ . To do so let’s subtract,

$z - \bar{z} = x + iy - x + iy = 2iy.$

Thus, $y = \frac{z - \bar{z}}{2i}$ and after applying this result to Euler’s formula we get,

$\boxed{\sin{(\theta)} = \frac{e^{i\theta}- e^{-i\theta}}{2i}}.$

The algebra will be a little messier than it was for cosine, because of the extra minus sign and the $i$ in the denominator. I wanted to leave the rest as a challenge for the reader, but I thought I would at least type out the steps you’d need to carry out. There will be no explanation, just the algebra, your welcome!

$\sin{(a)}\sin{(b)} = \Big(\frac{e^{i a}- e^{-i a}}{2i}\Big)\cdot \Big(\frac{e^{i b}- e^{-ib}}{2i}\Big)\\\textit{ }\qquad\qquad\;\;\;\; = \frac{1}{4i^2} \Big(e^{i(a+b)} - e^{i(a-b)}-e^{i(-a+b)}+e^{i(-a-b)}\Big) \\ \textit{ }\;\\\textit{ }\qquad\qquad\;\;\;\; = \frac{-1}{4} \Big(e^{i(a+b)} - e^{i(a-b)}+e^{-i(a+b)}-e^{-i(a-b)}\Big) \qquad \mathrm{after}\;\mathrm{some}\;\mathrm{rearranging}\\ \textit{ }\; \\\textit{ }\qquad\qquad\;\;\;\; = -\frac{1}{2}\Bigg(\Big(\frac{e^{i(a+b)} + e^{-i(a+b)}}{2}\Big) - \Big(\frac{e^{i(a-b)} + e^{-i(a-b)}}{2}\Big)\Bigg)\\ \textit{ }\;\\\textit{ }\qquad\qquad\;\;\;\;\; =-\frac{1}{2}\Big(\cos{(a+b)}-\cos{(a-b)}\Big)\\ \textit{ }\;\\\textit{ }\qquad\qquad\;\;\;\;\; =\frac{1}{2}\Big(\cos{(a-b)}-\cos{(a+b)}\Big).$

And just like that,

$\boxed{\sin{(a)}\sin{(b)} = \frac{1}{2}\Big(\cos{(a-b)}-\cos{(a+b)}\Big)}.$

Pythagorean Theorem

We’ve already considered the sum and difference of $e^{i \theta}$ and $e^{-i \theta}$ , now it’s time to consider their product!

You’re probably familiar with the Pythagorean theorem and how it relates the side lengths of a right triangle. Euler’s formula allows for a quick “proof”, of sorts, of the Pythagorean theorem. It’s time to take the product of $e^{i \theta}$ and $e^{-i \theta}$ . First, note using exponents rules,

$e^{i \theta}e^{-i \theta} = e^{i(\theta - \theta)} = e^0= 1$

Furthermore, using Euler’s formula,

$e^{i \theta}e^{-i \theta} = \Big( \cos{(\theta)} + i \sin{(\theta)}\Big) \Big( \cos{(\theta)} - i \sin{(\theta)}\Big) \\ \textit{ } \qquad \;\,= \cos{(\theta)}^2 + \sin{(\theta)}^2$

Thus,

$\cos{(\theta)}^2 + \sin{(\theta)}^2 =1.$

Which is the unit circle version of the Pythagorean theorem. How wonderful yet again!

Demoivre’s Theorem

Most people have not heard of Demoivre’s Theorem but it’s also a great theorem regarding complex numbers. Before we state what, it tells us, let us first mention polar form for complex numbers.

Let $z = x+iy$ be a complex number. We can represent a complex number as a point in a plane

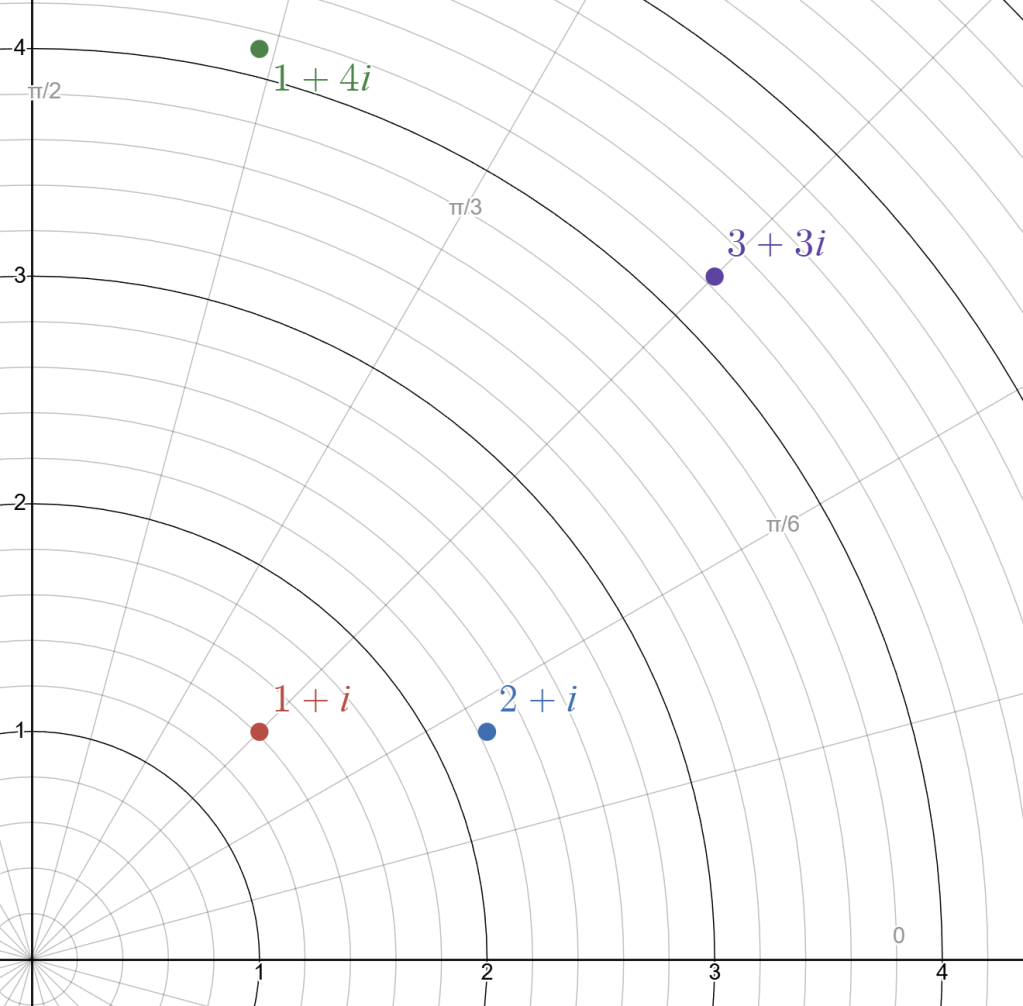
Above we plotted four complex numbers. The way we did so was by taking $z = x+iy$ and plotting it at $(x,y)$ . In this way the horizontal line is the real axis, and the vertical line is the imaginary axis. For example, $2+i$ was plotted at $(2,1)$ and $1+i$ was plotted at $(1,1).$ However, an equally good way to visualize the complex number $1 + i$ is to use polar (or circular) coordinates.

Picture a circle centered at the origin that is large enough so that way $(x,y)$ lies on the circle. Denote the radius of this circle $r.$ Also, denote the angle between the point $(x,y)$ and the positive $x$ -axis by $\theta$ . Polar coordinates exchange $x$ and $y$ with $r$ and $\theta$ .

For example, $(1,1)$ would be on a circle of radius: $\sqrt{x^2+y^2} = \sqrt{2}$ . The angle off the $x$ -axis is found using $\tan{(\theta)} = \frac{y}{x} = 1$ . Thus, $\theta = \arctan{\left( 1\right)} = \frac{\pi}{4}$ (you can also find the angle by looking at the figure above).²

We are therefore led to the following conclusion:

$z = x+iy = r \,\Big( \cos{(\theta)} + i \sin{(\theta)}\Big)$

where $r =\sqrt{x^2+y^2}$ and $\theta = \arctan{\left( \frac{y}{x}\right)} .$ ***This was rushed so if it’s confusing consider checking out one of the links below for further learning!***

Now imagine the situation where you wanted to raise some complex number to a large power $n$ . It would not be much fun to have to foil out $(x+iy)^n.$ This is where DeMoivre’s theorem comes in handy. It states: For any integer $n$ ,

$\Bigg[ r \,\Big( \cos{(\theta)} + i \sin{(\theta)}\Big) \Bigg]^n = r^n \,\Big(\cos{(n\theta)} + i \sin{(n\theta)} \Big)$

The usual proof uses induction and requires some comfort with trig. But, using Euler’s formula it is a one-line proof!

$\Bigg[ r \,\Big( \cos{(\theta)} + i \sin{(\theta)}\Big) \Bigg]^n =\Big(r e^{i\theta}\Big)^n = r^n e^{in\theta}= r^n \,\Big(\cos{(n\theta)} + i \sin{(n\theta)} \Big)$

BOOOM!

Concluding Remarks

Euler’s formula is a critical tool for complex analysis, algebra, and basically anything you want to do that needs complex numbers. Not only this, it also leads to the most beautiful equation ever, called Euler’s Identity:

$e^{i \pi}+1 = 0.$

Which brings together $e$ from calculus, $\pi$ from geometry, $0$ and $1$ from arithmetic into one formula.

There are numerous sources out there to learn more about complex numbers and how useful they are. However, using it as a tool for fast trigonometry is useful for anyone and not just those who study complex numbers!

For those who want more information about complex numbers feel free to peruse these sources. As always, I hope you have a kick in the discovery along the way!

Further Fun for the Fundamentals

Veritasium’s (Video): How Imaginary Numbers Were Invented
Numberphile (Video): Euler’s Formula
Brillant (Article): Polar Coordinates | Brilliant Math & Science Wiki
Numberphile (Video): Complex Numbers are Awesome
Numberphile (Video): e (Euler’s Number)
3Blue1Brown (Video): What’s so special about Euler’s number e? | Chapter 5, Essence of calculus
3Blue1Brown (Video): Complex number fundamentals | Ep. 3 Lockdown live math
3Blue1Brown (Video): What is Euler’s formula actually saying? | Ep. 4 Lockdown live math
Khan Academy (Video and Problems): Complex numbers | Algebra 2 | Math | Khan Academy
Stan Up Maths(Video): Complex Fibonacci Numbers?

Awesome and Advanced

Footnotes:

Let $x$ and $y$ be real numbers. For some complex number $z=x+iy$ you get the complex conjugate denoted by $\bar{z}$ or $z^*$ by simply changing the sign on the imaginary part. Some examples are the following:
$z =\;\;2+3i \qquad \mathrm{and} \qquad \bar{z} =2-3i$ .
$z = 101 - \frac{1}{2}i \qquad \mathrm{and} \qquad \bar{z} = 101 + \frac{1}{2}i$
$z = \frac{1+i}{2} \qquad \mathrm{and} \qquad \bar{z} = \frac{1-i}{2}$
$z=e^{i \theta} = \cos{(\theta)} + i \sin{(\theta)}\qquad \mathrm{and} \qquad \bar{z} = e^{-i \theta} = \cos{(\theta)} - i \sin{(\theta)}$
The reason why people care about the complex conjugate is because of what the product of $z$ and $\bar{z}$ is. If you carry out the foiling and cancelations you will conclude that $z\bar{z} = x^2 + y^2$ . Which is a real number and that it looks like the Pythagorean theorem!
↩︎
Note this angle is not unique since $\tan{\left(\frac{\pi}{4}\right)} = \tan{\left(\frac{9\pi}{4}\right)} = \tan{\left(\frac{\pi}{4}+n\pi \right)} =1.$ ↩︎

One response to “Euler’s Formula as a Tool for Fast Trigonometry”

Trig Rules the Old Fashioned Way – A Kick in the Discovery

June 21, 2025

[…] Last week we learned some tricks to derive some trigonometry identities quickly while using Euler’s formula; however, once I finished writing it, I wanted to prove the same rules using triangles and geometry! I thought it would be fun and boy howdy was I right! […]

LikeLike