What Comes Next: 1, 2, 4, 8, 16, … hint it’s not 32

A Kick in the Discovery

, , ,

Let’s get Real… Analysis (Part 1): Super Supremum and Infamous Infimum

Published by

Valt

on

Mathematicians love to generalize/extend ideas and concepts. There seems to be no limit to their creativity in finding ever more generalized versions of everyday concepts. From exponentiation first being shorthand for repeated multiplication, e.g. 2^3 = 2\times 2\times 2\times = 8, to extending exponentiation to include rational exponents like 2^{1/4} = \sqrt[4]{2}\approx 1.189207115\cdots. And then again to something like 2^{\sqrt{2}}\approx 2.66514414269.... What on earth does 2^{\sqrt{2}}\approx 2.66514414269... mean????

Today we are going to see how mathematicians, in the attempt to make calculus rigorous, extended the concepts of a maximum and a minimum element in a set.

Supremum and Infimum the Basics

Ok, since we plan on extending the idea of a maximum and minimum values of a set, we should state explicitly what it means for a number M to be a maximum of a set S. Our focus in on sets of real numbers, i.e. subsets of \mathbb{R}.

Definition: (Maximum) Let S be a nonempty subset of \mathbb{R}. We call M is the maximum value in S if

  1. M is in S and
  2. for any number n in S we have M \geq n.

We denote the maximum value by \max{(S)} = M.

For example, if S=\{ 1,2,3,4\} then \max{(S)} = 4 since 4\in S and every other integer in S is less than or equal to 4. Likewise, if our set is the interval S= [0,1] then \max{S} = 1.

Also, note that if S has a maximum, then there exist numbers that are larger than every number in S. Continuing with S=\{ 1,2,3,4\} and \max{(S)} = 4, the number 5 is larger than everything in S. We could say, S is bounded above by 5.

Not too bad so far.

Most sets don’t have a maximum value though. There are boring examples of this like the integers \mathbb{Z}. Since there is no upper limit to how large an integer can get we say that \mathbb{Z} doesn’t have a maximum. But if we wanted we could just define its maximum to be infinity. The real fun happens when we have a set that is bounded (above). For example,

A=\{ \frac{1}{2},\frac{2}{3},\frac{3}{4},\frac{5}{6},\cdots\} or the open interval I=(0,1).

First, notice that neither set has a maximum value

\max{(A)}=DNE and \max{(I)}=DNE.

For example, consider 0.9999999999. If we naively said that 0.9999999999 was either \max{(A)} or \max{(I)}, then we’d be wrong since \frac{99999999999999999999}{100000000000000000000} is in both S and I and is larger than 0.9999999999. New idea, what about \max{(A)}=1 or \max{(I)}=1 . Every number in A and I is less than 1, but 1 isn’t in either set so 1 cannot be their maximum. We can’t seem to win!

Even though neither set has a maximum, we can still find numbers that bound both sets (there are numbers larger than every element in A and I). For example, 1 is larger than every number in either set. This is similar to the fact that sets with a maximum are bounded above as well.

Now, did you notice that 1 seems to be a special value for both A and I? Both sets have the property that you can find numbers as close to 1 as you want (as long as they are less than 1).

For these two reasons we might say A and I seem to `want to have’ (but don’t have) 1 as their maximum. This is where we try to extend our notion of a maximum. We want to capture how 1 is like a pseudo maximum for A and I. To fully flesh out why 1 seems to be special, mathematicians invented what we call the supremum of a set. It turns out to be advantageous to first consider upper bounds of our sets A and I and then go from there.

Definition (Upper Bounds): Let S be a nonempty subset of \mathbb{R}. We call u an upper bound of the set S, if u\geq x for all x in S.

If the set S has an upper bound, then we say that S is bounded above. If there is no such u\in \mathbb{R}, then we say that S is unbounded above.

For example, 100 and 1.1 and 1.0001 and \pi and 1 are an upper bounds of A=\{ \frac{1}{2},\frac{2}{3},\frac{3}{4},\frac{5}{6},\cdots\} and the open interval I=(0,1).

Our next step is to turn our attention to a very special upper bound, the least upper bound.

Definition (Supremum): Let S be a nonempty subset of \mathbb{R}. We call \alpha the least upper bound of S if,

  1. \alpha is an upper bound of S and
  2. for any upper bound u of S we have \alpha \leq u.

If S is unbounded above, then we say that the supremum of S is infinity.

We denote that supremum of S by \sup{(S)}.

That’s it! Let’s look at some examples:

  • If A=\{ \frac{1}{2},\frac{2}{3},\frac{3}{4},\frac{5}{6},\cdots\}, then \sup{(A)}= 1
  • If B=\{ 1,2,3,4\}, then \sup{(S)}= 4
  • If C=\{ 1,2,3,4, 4.9, 4.99, 4.9999, 4.999999, \cdots\}, then \sup{(C)}= 5.
  • If \mathbb{N}=\{ 1,2,3,4,\cdots\}, then \sup{(\mathbb{N})}= \infty
  • If I=(0,1), then \sup{(I)}= 1
  • If I_2= [0,1], then \sup{(I_2)}= 1

The supremum captures the idea that some sets “want to” have a maximum but never reach it. They get closer and closer to that almost maximum value, this value ends up being the set’s least upper bound, i.e it’s supremum.

Finding and then Proving the Supremum Analytically

I find that most confusion arises in proving our assertions about what the supremum of a set is. For example, how do we prove that \sup{(A)}= 1 for the set A=\{ \frac{1}{2},\frac{2}{3},\frac{3}{4},\frac{5}{6},\cdots\}? It seems obvious that it should be 1, however, obvious statements are usually the toughest to prove.

For this reason, we want an analytic way to understand the supremum. This will not only be good practice for up-and-coming topics like sequence limits, functional limits, and continuity, but it will also make our lives easier later on when we need to prove statements about the supremum.

Let’s trial some ideas.

Ideas are good

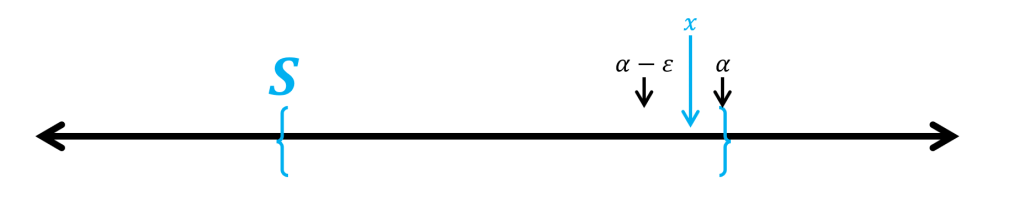
Let’s say that some set S has \sup{(S)}= \alpha. Our goal is to find an analytic way to prove this statement. Since we are trying to prove that \alpha is a least upper bound of S, what can we say about the slightly smaller \alpha - 0.1? Well, since \alpha is the least upper bound and \alpha -0.1 < \alpha we know that \alpha -0.1 is not an upper bound of S. We have to be careful, we cannot say that \alpha -0.1 is in our set S, but we can that that there should be some element x in S that is larger than \alpha -0.1 and less than or equal to \alpha.

If there wasn’t, then \alpha -0.1 would be an upper bound and this would contradict that \alpha was supposed to be the least upper bound.

Question: Was there anything special about subtracting 0.1? No! We could have subtracted 0.00000000000001 and the analysis would have been the same. This is the key idea behind the following theorem:

Theorem: (Proving Supremum using Analysis) Let S be a nonempty subset of \mathbb{R}. Then, \sup{(S)} = \alpha if an only if

  1. \alpha is an upper bound of S and,
  2. for any \varepsilon >0 there exists a x in S such that x>\alpha -\varepsilon.

This probably seems like an overly complicated way to understand supremum, but all the theorem is trying to convey is the idea that we discussed right before it. That is, if we subtract any positive quantity (\varepsilon) away from \alpha, then this smaller number (\alpha -\varepsilon) is no longer an upper bound. And since it’s not an upper bound, there should be an element of S that is larger than \alpha - \varepsilon, i.e. there is an x\in S such that \alpha - \varepsilon < x \leq \alpha.

Proof: Let S be a nonempty subset of \mathbb{R}. Since this is an if and only if statement, we have two directions to prove. Let’s do the forward direction first.

Forward: If \sup{(S)} = \alpha, then (1) \alpha is an upper bound of S and, (2) for any \varepsilon >0 there exists a x in S such that x>\alpha -\varepsilon.

Let \sup{(S)} = \alpha. By the definition of a supremum \alpha is an upper bound of S. That takes care of (1). To take care of (2), let’s assume for a contradiction that it wasn’t true that for any \varepsilon >0 there exists a x in S such that x>\alpha -\varepsilon. Or, equivalently it is true that

there exists an \varepsilon >0 such that for all x in S we have x\leq \alpha -\varepsilon.

But, then \alpha -\varepsilon is an upper bound (check the definition of an upper bound). This contradicts that \sup{(S)} = \alpha and concludes the forwards direction.

Backward: If \alpha satisfies the two properties: (1) \alpha is an upper bound of S and, (2) for any \varepsilon >0 there exists a x in S such that x>\alpha -\varepsilon, then \sup{(S)} = \alpha.

Let the \alpha satisfies the two properties: (1) \alpha is an upper bound of S and, (2) for any \varepsilon >0 there exists a x in S such that x>\alpha -\varepsilon. We need to show that \alpha is the supremum of S.

Property (1) takes care of the first part in the definition of supremum. What we have to do is show that \alpha is the least upper bound. To this end, let’s assume for a contradiction that \alpha was not the least upper bound. This would imply that there is some other upper bound \gamma such that \gamma<\alpha . Since property (2) says: for all \varepsilon >0 blah blah blah, we can choose a specific value for \varepsilon >0 to reach our contradiction.

We let \varepsilon = \alpha - \gamma >0. By property (2) there is some x in S such that

x>\alpha -\varepsilon = \gamma.

But wait, \gamma was supposed to be an upper bound, and yet we found something larger than \gamma in S. This is our contradiction!

And just like that we conclude our proof.

\square

Supremum and The Real Numbers

A critical fact is that the real numbers are closed with respect to the supremum. By this, we mean that any subset of the real numbers will have a supremum that is either a real number or infinity. We don’t need to invent more numbers to account for the supremum.

This is not a fact that the rational numbers enjoy. For example, if we take more and more digits from the square root of 2’s decimal expansion, we find that the following set of rational numbers

\{1, \frac{14}{10},\frac{141}{100},\frac{1414}{1000}\frac{14142}{10000},\cdots \}

has a supremum of \sqrt{2} which we know is not a rational number. Moral: It’s possible for a bounded subset of rational numbers to have a supremum that is not a rational number. This is NOT possible for subsets of real numbers. Every bounded subset of real numbers will have it supremum in \mathbb{R}.

Theorem/Pseudo-Axiom (Least Upper Bound Property of \mathbb{R}) Let S be a non-empty subset of real numbers that is bounded above. Then \sup{(S)} exists and is a finite real number.

See Least-upper-bound property – Wikipedia for more details and references.

In fact, I misled you at the beginning. We motivated the supremum by saying that it was a generalization of the maximum of a set; this is not the whole story.

Say we were interested in constructing the real numbers by extending the rational numbers. To do this we’d want `add in’ the irrational numbers `missing’ from \mathbb{Q} into \mathbb{R}. This is not easy, though. How do you say you need to add in \sqrt{2} without knowing what \sqrt{2} is? The trick is to think of the supremum as \sqrt{2}:

\sup{(\{x\in \mathbb{Q} \;:\; x^2 \leq 2 \})}.

The beauty of this idea is that we don’t need to explicitly know what numbers are missing from the rational numbers! We don’t actually reference irrational numbers, only the rational ones in some set. And since all we know are rational numbers this is great! We then construct the missing numbers like \sqrt{2} by making sets like the one above. We are referencing something outside our set by focusing on upper bounds!! But this is taking us to far a field for where I was hoping to go, so just make a note of this fact.

Archimedean Property

Let’s use the supremum and the least upper-bound property to prove what is known as the Archimedean Property.

Theorem (The Archimedean Property): For any x real number there exists a natural number n such that:

n>x.

Proof: Let x be a real number. If x\leq 0, then the natural number 1 does the job. So lets assume that x>0.

For the hope of a contradiction, let’s assume that it wasn’t true that there was natural number n such that n>x. Or, that is is true that for all natural numbers n we have n\leq x.

This would mean that the set of natural numbers \mathbb{N} is both a subset of \mathbb{R} and bounded above by x. By the least upper bound property \sup{(\mathbb{N})} exists. Let’s denote it by M.

By using \varepsilon=1>0 and the definition of a supremum, there exists a natural number N such that N > M -1. Equivalently, N+1>M. Do you see the contradiction? Since N is a natural number, so is N+1. But, then we just found a natural number larger than the supremum of natural numbers M. Hence a contradiction Eurika!

\square

Examples Galor

Let’s prove some of the claims that we made earlier. In all the proofs that follow, we will want to show that for any \varepsilon >0 there exists a x in S such that x>\alpha -\varepsilon. We can think of this task as a game! Someone gives us an \varepsilon>0 and we must find an x in S that will satisfy x>1 -\varepsilon.

The hard part is that our x must work any \varepsilon>0 given to us. The trick is to have x depend on \varepsilon. Let’s see in the following examples.

If I= (0,1), then \sup{(I)}= 1

Scratch Work: Well, (0,1) is defined to be all real numbers x that are in between 0 and 1 (not including 0 and 1) or, in a more mathy way: (0,1) contains the real number x such that 0< x< 1. So, by the definition of the set that we see that 1> x for all x in S. Thus, 1 is an upper bound.

We now want to show that for any \varepsilon >0 there exists a x in S such that x>1 -\varepsilon. So, let’s work with x>1 -\varepsilon. Since \varepsilon >0 we know that 0<\frac{\varepsilon}{2}<\varepsilon. This is great! If we have x = 1 -\frac{\varepsilon}{2}> 1-\varepsilon. So we’re done, right?

Not quite, since we are given \varepsilon we have no control over how large it is or small it is. This can cause issues, for example, what would x be if \varepsilon = 3? Well, x = 1 -\frac{3}{2} = -\frac{1}{2} and x is no longer in our set! For this reason, we need to be a little more caution and do a kind of case-by-case definition.

Proof: Let \varepsilon > 0 and x = \max{(\{\frac{1}{2},1 -\frac{\varepsilon}{2}\})}. As mentioned, 1 is an upper bound of S. To see property (2) observe for 0<\varepsilon<1 we have x = 1 -\frac{\varepsilon}{2} so that \frac{1}{2}<x<1 (and thus in the interval (0,1)) and,

x = 1 -\frac{\varepsilon}{2}> 1-\varepsilon.

On the other hand, when \varepsilon \geq 1 we have

x = \frac{1}{2} >0= 1-\varepsilon.

In either case we have shown x = \max{(\{0,1 -\frac{\varepsilon}{2}\})} is in our set and x > 1-\varepsilon. Which is what we set out to do.

\square

If A=\{ \frac{1}{2},\frac{2}{3},\frac{3}{4},\frac{5}{6},\cdots\}, then \sup{(A)}= 1

Scratch Work: The strategy is the same. Since every element in A=\{ \frac{1}{2},\frac{2}{3},\frac{3}{4},\frac{5}{6},\cdots\} is less than 1, we must now show that for any \varepsilon >0 there exists a x in A such that x>1 -\varepsilon.

As a hint, rewrite every element in S to be in the form 1-\frac{1}{n} and recall the Archimedean property.

Proof: Let \varepsilon >0. First, observe that every element in A is equal to 1-\frac{1}{n}, for some natural number n. In this form, we can see that 1 is indeed an upper bound of A.

Next, observe that for our \varepsilon >0, there exists a natural number N such that \frac{1}{\varepsilon} <N, by the Archimedean property. Equivalently, there exists a natural number N such that \frac{1}{N} <\varepsilon. Thus, for x = 1-\frac{1}{N} we have x\in S and

x = 1-\frac{1}{N}> 1- \varepsilon.

This concludes the proof!

\square

A Quick Comment

Did you notice anything about how we started our two proofs above? No? Double check!

We started each proof by saying, “Let \varepsilon >0. ” This is very important because we want everything, we conclude to be independent from what \varepsilon equals. And to do this, we start by saying, “Let \varepsilon >0” and then deduce from there.

Connecting Supremum to the Maximum of a Set

We began with the motivation of generalizing maxima and minima of sets. So it better be the case that when a set has a maximum value it equals it’s supremum. Indeed this is the case.

Theorem (Supremum and Maximum): Let S be a nonempty, bounded, subset of \mathbb{R}. If \max{(S)} exists, then \sup{(S)} = \max{(S)}.

Proof: Let S be a nonempty, bounded subset of \mathbb{R} such that and \max{(S)} exists. Let’s denote \max{(S)} by M. We must show that \sup{(S)} = M.

Let \varepsilon>0 and observe that M is an upper bound since M\geq m for all m in S. Finally, since M \in S we have M> M - \varepsilon. Done!

\square

If I_2= [0,1], then \sup{(I_2)}= 1

Proof: Observe by definition \max{(I_2)}= 1 \in S. Thus, \sup{(I_2)}= 1.

\square

Ok What about the Infimum???

Up to now we have focused on the supremum and maximum. The infimum is to the minimum as the supremum is to the maximum. Meaning everything we stated has an analogous definition or theorem:

Definition: (Minimum) Let S be a nonempty subset of \mathbb{R}. We call m is the minimum value in S if

  1. m is in S and
  2. for any number n in S we have m \leq n.

We denote the maximum value by \min{(S)} = m.

Definition (Lower Bounds): Let S be a nonempty subset of \mathbb{R}. We call l a lower bound of the set S, if l\leq x for all x in S.

If the set S has a lower bound, then we say that S is bounded above.

Definition (Infimum): Let S be a nonempty subset of \mathbb{R}. We call \beta the greatest lower bound of S if,

  1. \beta is a lower bound of S and
  2. for any lower bound l of S we have \beta \geq l.

If S is unbounded below, then we say that the supremum of S is negative infinity.

We denote that supremum of S by \inf{(S)}.

Theorem: (Proving Infimum using Analysis) Let S be a nonempty subset of \mathbb{R}. Then, \inf{(S)} = \beta if an only if

  1. \beta is a lower bound of S and,
  2. for any \varepsilon >0 there exists a x in S such that x<\beta +\varepsilon.

Corollary (Greatest Upper Bound Property of \mathbb{R}) Let S be a non-empty subset of real numbers bounded from below. Then \inf{(S)} exists and is a finite real number.

*Note this is a corollary to Theorem/Pseudo-Axiom (Least Upper Bound Property of \mathbb{R}) *

Theorem (Infimum and Minimum): Let S be a nonempty, bounded, subset of \mathbb{R}. If \min{(S)} exists, then \inf{(S)} = \min{(S)}.

The proofs are the same as those given for the supremum, so I defer them to you! I have to leave you something to practice with!

Closing Remarks

This article was a very, very non-standard way to describe the supremum and infimum of a set. However, I think it is instructive to build intuition. If you go to any other book on the subject, you aren’t likely to find a description like this. This is why I wrote it, after all, there are many great books on this subject already!

Oh, and at the start I asked: What on earth does 2^{\sqrt{2}}\approx 2.66514414269... mean???? One way we can define what it means is the following:

2^{\sqrt{2}} := \sup{\left\{2^x \,:\, x^2<2 \right\}},

where x\in\mathbb{Q}.

We’ll next encounter supremum and infimum when we start to look at sequences and limits.

Put your proofs for the infimum cases in the comments below!

4 responses to “Let’s get Real… Analysis (Part 1): Super Supremum and Infamous Infimum”

  1. Let’s Get Real… Analysis (Part 3.2) Uniqueness of Limits – A Kick in the Discovery Avatar
    Let’s Get Real… Analysis (Part 3.2) Uniqueness of Limits – A Kick in the Discovery

    […] meet again in our real analysis series! In part 1 we learned about the supremum and infimum and then in part 2 we learned about sequence limits. Part 3 has been broken up into two parts: 3.1 […]

    Like

    Reply
  2. Let’s Get Real… Analysis (Part 5): the Monotone Convergence Theorem – A Kick in the Discovery Avatar
    Let’s Get Real… Analysis (Part 5): the Monotone Convergence Theorem – A Kick in the Discovery

    […] on to the proof, I recommend you review the concepts/definitions of a supremum and an infimum from part 1. We use them […]

    Like

    Reply
  3. Funky Functions and Cool Continuity! – A Kick in the Discovery Avatar
    Funky Functions and Cool Continuity! – A Kick in the Discovery

    […] . By the Archimedean property, there is some such that . With this in mind, define the […]

    Like

    Reply
  4. Let’s Get Real… Analysis (Part 9): limsup’s, liminf’s, and the Bolzano-Weierstrass Theorem – A Kick in the Discovery Avatar
    Let’s Get Real… Analysis (Part 9): limsup’s, liminf’s, and the Bolzano-Weierstrass Theorem – A Kick in the Discovery

    […] we can prove by noting that and for all . Thus, and by our theorem Proving Supremum Analytically (PSA for short) (or see footnote2) we are […]

    Like

    Reply

Leave a reply to Let’s Get Real… Analysis (Part 3.2) Uniqueness of Limits – A Kick in the Discovery Cancel reply