What Comes Next: 1, 2, 4, 8, 16, … hint it’s not 32

A Kick in the Discovery

, , ,

Newbie at Number Theory (Part 6): Fermat’s Fantastic Little Theorem

Published by

Valt

on

Today’s our sixth article in the series Newbie at Number Theory. Today, Fermat’s little theorem. If you’ve read all my articles, then you would have seen a proof using Lagrange’s theorem in the setting of group theory. This time however, we show a proof that uses only tools that we have learned in the last 5 articles.

We will give two proofs of this theorem, but first… what is the theorem? Instead of telling you, I want to give you a chance to get A Kick in the Discovery for yourself. So… try these out (even if you use Wolfram Alpha):

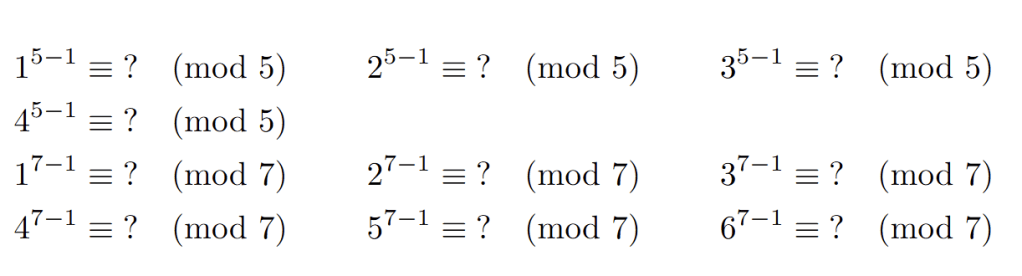
Notice anything? If so, make a conjecture! Then try to prove it!

Hint: 5 and 7 are primes. The exponents are (PRIME) – 1. Try these with composite modulus.

Fermat’s Little Theorem

What I hope you noticed is that every one of the above gave a^{p-1} \equiv 1 \pmod{p} . This happens for every prime and every a that is nonzero (mod p).

Fermat’s Little Theorem: Let p be prime and let a \not\equiv 0 \pmod{p}, then

a^{p-1} \equiv 1 \pmod{p}.

Equivalently, for any a,

a^{p} \equiv a \pmod{p}.

Proof 1: (Click in the Discovery)

This one is really snazzy! It’s exactly the same idea that we used when we proved Fermat’s little theorem here. But this time without all the group theory shenanigans.

Let p be prime and a \not\equiv 0 \pmod{p}. Consider the integers in the set S=\{1,2,3,\cdots,(p-1)\} times a .

S_a = \{1a\;,\;2a\;,\;3a\;,\;\cdots\;, \;(p-1)a \}

We claim that all of these integers are different (mod p). To see this, let na \equiv ma \pmod{p} with n and m being such that 1\leq m\leq n \leq p-1 (we do this so that way na and ma are in the set above). Then, subtracting ma from both sides,

na-ma =(n-m)a \equiv 0 \pmod{p},

implying that p\mid(n-m) or p\mid a (by Euclid’s Lemma). But since a \not\equiv 0 \pmod{p} it must be that p\nmid a and hence p\mid(n-m). But recall that we chose 1\leq m\leq n \leq p-1 , meaning that 0\leq n-m < p-1. And note that no positive integer less than p is divisible by p. Thus, p\mid(n-m) and 0\leq n-m < p-1 imply n-m = 0 or n=m. Consequently, na=ma.

Recap: We just proved that every integer in the set below is distinct (mod p), can you see why?

S_a = \{1a\;,\;2a\;,\;3a\;,\;\cdots\;, \;(p-1)a \}

Let’s reduce this set of integers (mod p). Since there are p-1 distinct integers (mod p) in S_a , it must be that S_a \pmod{p} is congruent to the set S=\{1,2,3,\cdots,(p-1)\} , with the elements not necessarily in the same order.1 Why you ask? It’s because when you reduce the integers in S_a using (mod p) you must get one of the integers in S . And, since there are p-1 integers in both sets, they must be equal.

\{1a\pmod{p},2a\pmod{p},\cdots,(p-1)a \pmod{p}\} = \{1,2,3,\cdots,(p-1)\} .

How awesome is that????

Because of this the product of every integer in S_a must be congruent (mod p) to the product of every integer in S

1a\cdot2a\cdot3a\cdot4a\cdot5a\cdot\cdots\cdot(p-1)a \equiv 1\cdot2\cdot3\cdot4\cdot5\cdots (p-1) \pmod{p}.

Or using the factorial,

(p-1)!\cdot a^{p-1} \equiv (p-1)! \pmod{p}.

It sure would be nice if we could divide both sides by (p-1) !, but we both know that division doesn’t play nice with modular arithmetic. Unless… what we divide by is relatively prime with the mod number (aka p). But p is prime… and again no positive integer less than p is divisible by p, thus (p-1)! \not\equiv 0 \pmod{p} . Therefore, we can divide by (p-1) ! giving

a^{p-1} \equiv 1 \pmod{p}.

And we are done! On to proof 2.

\square

Proof 2: (Click in the Discovery)

I have a marvelous second proof of this theorem, but it’s too long and I could not fit it here.2

Closing Remarks

What a remarkable statement: a^{p} \equiv a \pmod{p} for all a and primes p. You might be wondering if composite numbers can get in on the fun??? Or does it only work mod a prime?

Give it a try! You’ll find that Fermat’s little theorem doesn’t work for composite moduli. However, Euler did find a generalization. But that’s a story for another day! See if you can work out what it might be!

See you next time!

Footnote:

  1. Note I am using loose language here. I am merely trying to say that \{1a\pmod{p},2a\pmod{p},3a\pmod{p},\cdots,(p-1)a \pmod{p}\} \\= \{1,2,3,\cdots,(p-1)\} . ↩︎
  2. How many of you saw this joke coming? ↩︎

One response to “Newbie at Number Theory (Part 6): Fermat’s Fantastic Little Theorem”

  1. Newbie at Number Theory (Part 9): Euler’s Little Theorem – A Kick in the Discovery Avatar
    Newbie at Number Theory (Part 9): Euler’s Little Theorem – A Kick in the Discovery

    […] you might have guessed, we’re going learn about Euler’s generalization of Fermat’s Little Theorem, that I’ve dubbed Euler’s Little Theorem. Note this is only what I call the theorem, […]

    Like

    Reply

Leave a reply to Newbie at Number Theory (Part 9): Euler’s Little Theorem – A Kick in the Discovery Cancel reply