A Kick in the Discovery

Last time we left off with a mystery… But before we get to that, a little introduction.

In your high school algebra class, you were probably given some equation like and asked to find some points that are on the line. Sometimes you might rearrange the equation to be in the form: to help out. So, for example, given you’d show was on the line.

Now, let’s ask a more difficult question.

Find all the integer solutions to the equation , if they exist. What makes this challenging is that we only want integers, so we can’t start dividing by 3 or 5, because then we get fractions. Not good.

So, I ask you:

How do we know there is even one solution? If there is, how do you find the solution? If there is a solution can there be more than one solution?

We will answer all these questions!

NOTE: When we say ‘solution’ we mean an integer solution.

Now back to the mystery from last time.

A Motivating Mystery (Taken From Here)

Let’s consider,

.

Are there any integer solutions? If so, can you find any? Give it a try!

I’ll wait…

Did you find any?

No?

Does that mean you didn’t try enough, or are there no solutions?

Ok, try this one, it’s almost the same:

.

Give it a go!

Did you find any this time?

Maybe x = -2 and y = 1: since . Or maybe you found x=3 and y=-1 since . Or maybe you found another one that wasn’t either of the two above!

The first equation has no solutions whereas the second one has infinitely many solutions.

What’s the problem with the first one, why is there no solution? If you haven’t had time to think about it, give it a few minutes. Once you think you have a guess, use it to guess whether has a solution.

Solution

Take a look at the left-hand and right-hand sides:

.

No matter what you choose for x and y, the left-hand side is even. The right-hand side is 1, which is odd. This is why there are no solutions. Since if there was a solution then we’d have the impossible statement: (Even Integer) = (Odd Integer).

Notice how this issue does not arise with , since the left-hand side can be odd or even. So, maybe if at least one of or is odd, then there is a solution to . If this is correct, we would be led to believe that has a solution.

There’s a problem because there is no integer solution to .

Why? Both and are both odd. What’s the issue?

The issue is not 15’s and 21’s even/odd-ness, but their divisibility by 3:

.

So it seems important to consider what numbers are a divisor of both and .

For another example, consider the situation when . Then and share a common factor 5 (or and ). So we can write: and , where and are integers. Thus,

We conclude that has no integer solutions. For if there was, then we’d conclude that is an integer: .

We therefore focus on finding when there are common factors between and . Here’s some new language:

Definition: We say two integers and are relatively prime (or coprime) if they share no factors. Or, more simply, when

So, we might conjecture something like this:

Conjecture: If the equation: has a solution, then and are relatively prime.

This is indeed true. Actually, it’s even stronger than that! But first, Bézout’s Identity.

Bézout’s Identity

Bézout’s Identity: Let and be integers. If , then the equation: has an integer solution.

Proof Idea: We are going to rely heavily on the Euclidean Algorithm, so I recommend you take a moment to recall the process of finding , for any and .

Here’s the color-coded schematic from last time:

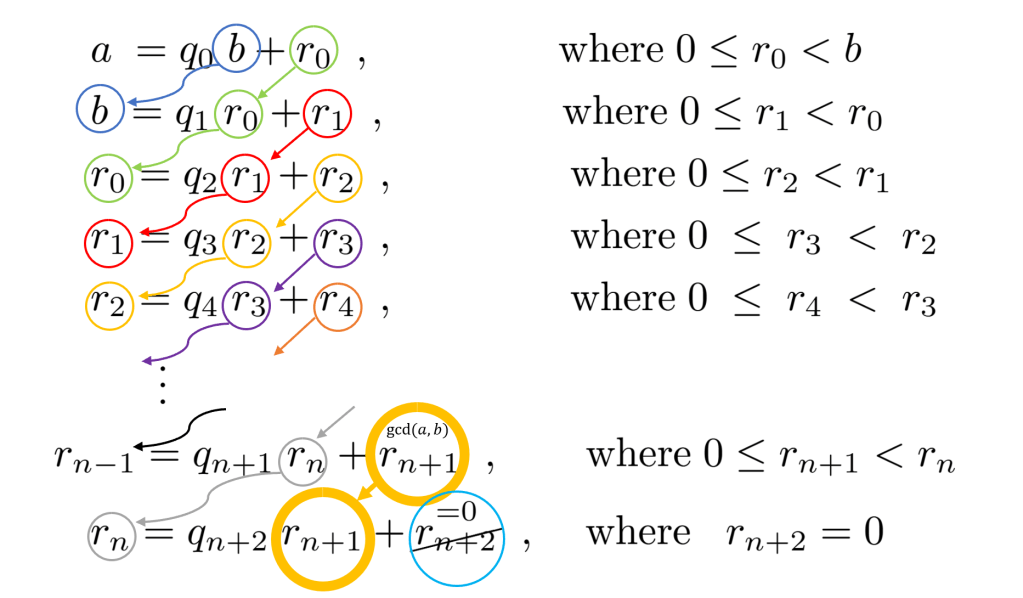
Since we want a solution to , having an expression for seems like a good place to start. Observe the second to last equation above. The greatest common divisor is the remainder in the second to last equation. Rearranging the second to last equation we get:

We ultimately want and in our solution equation for . Since they are in the first equation in the Euclidean Algorithm, let’s see if we can move upward in the algorithm by solving for remainders.

The line above the second to last equation but we can deduce it would have been . Again, let’s solve for the remainder

Wait, we can plug this into our expression ! This brings us closer to the step with and ,

Where we gathered all like terms.

Our game plan is to continue doing this until we reach the top equation with and . In other words, you just keep plugging in the next remainder until you reach the top! Once you do, you end up with an expression of the form:

Where the stuff and more stuff are integer expressions full of remainders ‘s and quotients ‘s.

Let’s do an example.

Example

Our aim to to find integers and such that

From last time, we saw by the following steps of the Euclidean Algorithm:

And since shows up in the third line, there will be three steps to find and .

Step 1: Solve the third line for .

.

Step 2: Solve the second line for its remainder aka 5,

and then plug this into step 1.

.

Step 3: Solve the first line for its remainder aka 6,

.

Plug this into the result of step 2.

.

And we’re done. We’ve found a solution: and .

.

Boo! No Proof!

We won’t give a detailed proof here of Bézout’s Identity. Mostly because it relies on the Euclidean Algorithm’s quotients and remainders to find and which means that the subscripts become messy. All we would need to do is formalize what we just did in the example.

Generalization

Bézout’s Identity has a more general form. What would happen if we tried to find a solution to the equation:

Where we still identify . Well, we know by Bézout’s Identity there is a solution to . Let’s denote this guaranteed solution by and so that

But, then multiplying every term by 10 gives:

Thus, and solve our new equation. Our more general form is the following Corollary:

Corollary: Let and be integers and . Then the equation: has an integer solution if and only if .

We did not go through a formal proof of Bézout’s Identity, nevertheless, we will use it in this proof.

Proof: (Click in the Discovery)

Proof: Let and be integers and . Since we are proving an if and only if statement, we have two directions to prove.

Forward: If has a solution in the integers, then

For the hope of a contradiction, assume that there is a solution to and . Denote the solution by and . What’s our contradiction? Well, we have the same situation we started with:

This is impossible, since if we divide the equation above by we’d have an integer on the left-hand side, whereas the right-hand side wouldn’t be an integer. We’d end up with the nonsensical statement: (Integer) = (Non-Integer).

Thus, it must be that .

Backward: If , then has a solution in the integers.

By Bézout’s Identity, we know there is a solution and to the equation . Since we can express in the following way, where is an integer. Thus, multiplying through by we get,

We have found a solution, ( and ), and we conclude our proof.

Zero or Infinite?

Ok, what’s left is there to do? We claimed at the beginning that has zero solutions and has infinitely many. We’ve done enough work to show that has no solution. Since and 2 does not divide 1, by the corollary there is no solution. But have we shown there are infinitely many solutions to ? No, not yet.

As we’ll see, there is either no solution or infinitely many solutions to , and nothing in between.

Theorem: Let and be integers and . If then the equation: has infinitely many integer solutions. In the case that there is no solution.

Intuition: We already know why there is no solution when , so let’s turn our attention to why there might be infinitely many solutions when . Since we already know that there is at least one solution when , can we generate another solution given a solution?

Let’s consider the examples we saw in the beginning,

and .

Let’s graph these two equations. Observe that every grid point hit (marked with an x) by the line is an integer solution to the equation of the line! This is the key idea.

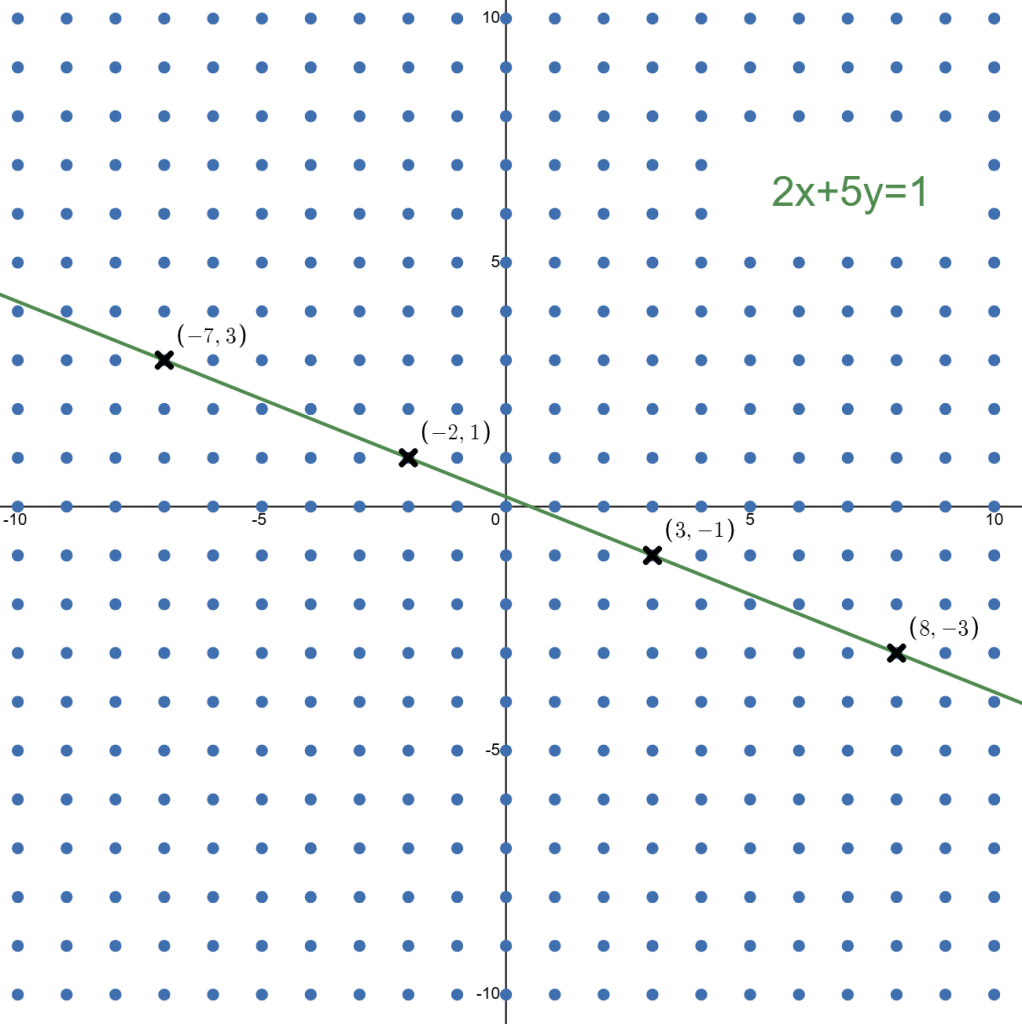
Turn your attention to the green line given by , because it actually has some solutions. Recall, we can rewrite the equation as, and therefore the slope of this line is . Thus, if and are integer solutions, then so are and , since

We chose to add 5k to on purpose, because the denominator of the slope is 5, it will cancel the 5 in the 5k giving an integer. So, we can see that having one solution results in infinitely many, since we can always shift to another grid point by the numerator and denominator of our rational slope.

Another way to see this is to add and subtract 10k to .

Where we chose 10 because And we again, see that and are solutions.

The red line never crosses any grid lines. (Why?)

Before we do the full proof, a quick lemma.

Euler’s Lemma

Here’s the idea. Take the integers 7 and 490. Since , we claim that any way we break down 490 into a product of its factors, we are guaranteed that 7 divides at least one of them. Let’s check when we write 490 as a product of two factors:

Let’s do another one. Consider again 490, but this time instead of 7 we use 10. In this case, every factor pair does not have at least one integer that is divisible by 10 even though .

What’s the difference? Take a look at the situations when we fail to have one integer that is divisible by 10, say the pair Observe that the two factors that make up 10 (ie 2 and 5) are split up between 14 and 35. And this doesn’t happen in situations like , because 2 and 5 are both contained inside 70.

If we can somehow guarantee that none of the factors of 10 split up or that they are all in one factor, then it must be that ten divides that factor. We do this by forcing one factor to be relatively prime with 10. Ie, if , and , then we know Just like with

This is known as Euler’s Lemma:

Euler’s Lemma: Let , , and be integers. If and . Then, .

Proof of Euler’s Lemma: (Click in the Discovery)

Let , , and be integers such that and . Since we know there is a solution (in the integers) to the following equation by Bézout’s Identity:

Multiplying through by b, we get,

Recall that , so that for some integer . Thus,

Since divides the left hand side, must also divide the right and side, aka .

We conclude .

Back to The Proof of Zero or Infinite?

Proof: (Click in the Discovery)

We’ve already took care of the second statement (when ), so we focus on the first part of the theorem (when ).

We are going to do a constructive proof of this theorem. We will find an expression for the infinitely many solutions to the equation .

Let and be integers, , and .

We already know that there is at least one set of solutions to , since . Call them and . We now employ a strategy that you might remember from high school algebra. We subtract the two equations,

Recall that and . We therefore can divide out by d,

This leaves the integer coefficients and .

Does it make sense that ? Since and shared at most a factor of d, by getting rid of d through division, what’s left share no factors. In symbols, as we said.

Rearranging our equation above to be,

We can see that the left-hand side is divisible by , implying that divides the right-hand side too. So, we have

and

and by Euler’s Lemma: . Or,

For some integer . This is our solution set for

Plugging our solution set for back into , we get our solution set for ,

Therefore, we have the two sets of solutions:

and

Since is any integer, we have infinitely many integer solution pairs.

Example

With our running example, , we already know that and is a solution. Plugging in these with , , , we get:

and

Or, simply

and

Let’s check different values of .

-1	8	-3
0	3	-1
1	-2	2
2	-7	3

And if you check the graph from earlier, these points are there.

 

It’s the Final Countdown… danananahhh

*I know you sang it in your head!*

Today’s post was much longer than usual! I hope you found it fun! Oh and the standard terminology for when we are finding integer solutions an equation is to call the equation a Diophantine equation.

There are many more Diophantine equations that we know how to solve. I recommend you check some out if you found this fun!

Your Own Problems

1. What are the integer solutions to ? This is the equation in the introduction.
2. We showed our solution set is given by and . Would and work too?
3. If you restrict x and y to be greater than or equal to 0, what different numbers n can you get in: ¹

Footnote:

1. Funnily enough, Numberphile put out a video the day I wrote this dealing with question 3. Watch it here. ↩︎