A Kick in the Discovery

For the long time readers of mine, you might recall what is called Euler’s Totient function. I recommend you take a look back at that previous article if you are not familar with some of $\phi$‘s properties:

Euler’s Totient Function: Let $n$ be a positive integer. Euler’s Totient Function $\phi$ is defined as,

$\phi(n) =\#\{m \in \mathbb{Z}\;:\;\gcd{(n,m)} = 1\;and \;0\lt m \leq n\}.$

Moreover, $\phi$ safitied the following properties:

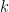
1. if is prime and is a positive integer,
2. If then,
3. If , then .
4. An equivalent way to express 3. is the following, $\phi(n) =\Big(p_a^{k_a} - p_a^{k_a-1}\Big)\cdots \Big(p_m^{k_m} - p_m^{k_m-1}\Big)$

What I would like to show you today, is one very interesting property that Euler’s totient function has. This was discovered by Gauss, so the theorem is kind of an Euler/Gauss team up. Also, the proof I will show you is a one-liner proof. I reccomend that you try to prove it on your own before you read the following one!

Theorem: Let $\phi$ be Euler’s totient function and $n\in \N.$ Then,

$n = \sum_{d\mid n}\phi(d).$

Where $\sum_{d\mid n}$ means, “sum over positive divisors $d$ of $n$.”

Let’s do a quick example. Let $n = 12.$ It follows that the divisors of 12 are, $d \in \{1,2,3,4,6,12\}.$ Thus,

$\sum_{d\mid 12}\phi(d) = \phi(1)+\phi(2)+\phi(3)+\phi(4)+\phi(6)+\phi(12)\\ \qquad\qquad\;\;\;\,=1 +1+2+2+2+4\\ \qquad\qquad\;\;\;\,=12.$

How remarkable!

Proof: (Click in the Discovery)

Here’s the idea. All of the factors of $n = p_1^{a_1}p_2^{a_2}\cdots p_k^{a_k}$ are a term in the following sum

$\Big(1+p_1+p_1^2+ \cdots + p_1^{a_1}\Big)\Big(1+p_2+p_2^2+ \cdots + p_2^{a_2}\Big)\cdots \Big(1+p_k+p_k^2+ \cdots + p_k^{a_k}\Big).$

Now, since $\phi$ has the property that $\phi(mn) = \phi(m)\phi(n)$ whenever $\gcd{(m,n)}=1,$we can deduce that

$\sum_{d\mid n} \phi(d) = \Big(\phi(1)+\phi(p_1)+\phi(p_1^2)+ \cdots + \phi(p_1^{a_1})\Big)\cdots \Big(\phi(1)+\phi(p_k)+\phi(p_k^2)+ \cdots + \phi(p_k^{a_k})\Big) \\\qquad\qquad\;\;= \Big(1+(p_1-1)+(p_1^2 - p_1)+ \cdots + (p_1^{a_1}- p_1^{a_1-1})\Big)\cdots \Big(1+(p_k-1)+(p_k^2 - p_k)+ \cdots + (p_k^{a_k}- p_k^{a_k-1})\Big)$

where we used (4.) in the properties of $\phi$. Observe that the above sums are telescoping. That is, we have a lot of cancelations!

$$\sum_{d\mid n} \phi(d) = \Big( p_1^{a_1}\Big)\cdots \Big( p_k^{a_k}\Big) = n.$$

Just like that, we’re done!

Oh, the one-liner version of the above proof is the following:

$\sum_{d\mid n} \phi(d) = \prod_{m=1}^k\sum_{i=1}^{a_m}\phi(p_m^{i}) = \prod_{m=1}^k\sum_{i=1}^{a_m}\Big(p_m^{i}-p_m^{i-1} \Big) = \prod_{m=1}^kp_m^{a_m} =n.$

Happy Thanksgiving (In the US)

I just want to end by saying thank you to all of you who read my silly little articles. I really appreciate it, and I get a lot of pleasure sharing math(s) with fellow nerds! See you next time!

Be Kind. Be Curious. Be Compassionate. Be Creative.

And Have Fun!