Integrability of Popcorn

Note that it’s assumed that the reader is familiar with Riemann Darboux integrals. This includes the next theorem:

Theorem (Integrals with Epsilon): Let $f$ be a bounded function on $[a,b].$ Then, $f$ is Riemann integrable if and only if for all $\varepsilon>0$ there exists a partition of $[a,b]$ such that

$U(f,P) - L(f,P) < \varepsilon.$

Where $U(f,P)$ and $L(f,P)$ are upper and lower sums.

Let’s Begin!

We’ve seen in the past (here) that Thomae’s Function aka The Stars over Babylon aka The Popcorn Function defined below is continuous on irrational numbers and discontinuous on the rational. Today, we will see that Thomae’s function is Riemann integrable using the above theorem.

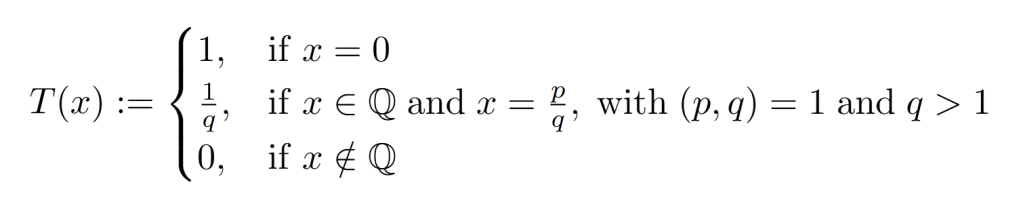
Very strange indeed. Here’s a great visualization of T before we study it.

By Smithers888 – Own work, Public Domain, https://commons.wikimedia.org/w/index.php?curid=4957683

***Note: The numbers $p$ and $q$ are integers***

Theorem (Popcorn is Integrable): Define $T:[0,1] \rightarrow \mathbb{R}$ as the restriction of the function above. Then $T$ is integrable.

Proof: (Click in the Discovery)

Let $\varepsilon>0.$ First, note that $T$ is bounded on $[0,1],$ so it makes sense to ask if it is Riemann integrable. We aim to prove that $T$ is integrable using by showing that there is a partition of $[0,1]$ such that,

$U(T,P) - L(T,P) < \varepsilon.$

To this end, consider the $x\in [0,1]$ such that $T(x)>\frac{\varepsilon}{4}.$ We first claim that there are only finitely many such $x.$ That is,

$\{x\in [0,1] \;:\; T(x)>\frac{\varepsilon}{4}\}$

is a finite set. To see this, go back to the definition of $T.$ Without loss of generality, suppose that $\varepsilon<1,$ then there are $x$ where,

$T(x)>\frac{\varepsilon}{4} \iff \Bigg( x=0\;\mathrm{or}\;x=p/q\;\mathrm{such}\;\mathrm{that}\;(p,q)=1\;\mathrm{and}\;0<q<4/\varepsilon\Bigg).$

Since there are only a finite number of integers $0<q<4/\varepsilon$ there is only a finite number of $x\in [0,1]$ such that $T(x)>\frac{\varepsilon}{4}.$ Let’s denote them, $a_1,a_2,\cdots, a_k.$

Next, we claim that $L(T,P)=0$ for all partitions of $[0,1].$ This follows from the fact that for all subintervals $[x_{i-1},x_i]\subset [0,1]$ there is an irrational number $c\in [x_{i-1},x_i]$ so that $\inf{\{T(x)\;:\;x\in [x_{i-1},x_i]\}} = T(c) = 0.$ It follows that $L(T,P)=0.$

Thus, our task reduces to finding a partition $P_{\varepsilon} = \{x_0,x_1,\cdots,x_n\}$ of $[0,1]$ such that $\textit{ }\;\; U(T,P)<\varepsilon.$ With this goal in mind, consider the following partition,

$P_{\varepsilon} =\{0,a_1 - \frac{\varepsilon}{4k},a_1 + \frac{\varepsilon}{4k},a_2 - \frac{\varepsilon}{4k},a_2+ \frac{\varepsilon}{4k},\cdots, a_k - \frac{\varepsilon}{4k},a_k + \frac{\varepsilon}{4k},1 \}$

Note, for all intervals of the form: $[a_i - \frac{\varepsilon}{4k},a_i+ \frac{\varepsilon}{4k}]$ , we have $\varepsilon/4<T(x) \leq 1.$ Also, for the intervals of the form $[a_i + \frac{\varepsilon}{4k},a_{i+1}- \frac{\varepsilon}{4k}]$ , we have $T(x)<\varepsilon/4.$ Let $M_i:= \sup{\{ T(x) \;:\;x\in [x_{i-1},x_i]\}}$ , it follows,

$U(T,P_{\varepsilon} ) = \sum_{i=1}^{2k+1} M_i \cdot(x_i - x_{i-1}) \\ \\\text{ }\qquad\;\;\;\;\;< \Big(\frac{\varepsilon}{4}\Big)\Big(a_1 - \frac{\varepsilon}{4k}\Big) +\Big(\frac{\varepsilon}{4}\Big)\Big(1-a_k - \frac{\varepsilon}{4k}\Big)+ \sum_{j=1}^{k-1}\frac{\varepsilon}{4} \Big(a_{j+1} - a_{j} - \frac{\varepsilon}{2k}\Big) \\ \\\text{ }\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\;\;\;\; +\sum_{j=1}^{k} 1\left(\frac{\varepsilon}{2k}\right)$

Where the first line of terms come from the intervals $[x_{i-1},x_i]$ that do not contain any $a_j.$ For all these intervals we use that $T(x)<\varepsilon/4.$ The last sum is for the intervals that contain the $a_j.$ We use 1 as an upper bound of $T.$

Note all the cancelation that happen between the terms with $a_i,$

$U(T,P) < - \frac{\varepsilon^2}{16k}+ \frac{\varepsilon}{4} - \frac{\varepsilon^2}{16k} - \left(\frac{\varepsilon^2}{8k}\right)\left(k-1\right) - \left(\frac{\varepsilon}{2k}\right)\left(k\right)\\ \\\text{ }\qquad\;\;\;\; = -\frac{\varepsilon^2}{8k}+\frac{\varepsilon}{4}-\frac{\varepsilon^2}{8}+\frac{\varepsilon^2}{8k} + \frac{\varepsilon }{2} \\ \\\text{ }\qquad\;\;\;\; < \frac{\varepsilon}{4}+\frac{\varepsilon}{2} -\frac{\varepsilon}{8},\qquad\qquad \mathrm{since}\;\varepsilon<1\\ \\\text{ }\qquad\;\;\;\; <\varepsilon.$

Thus, $T$ is Riemann integrable.

$\square$

That’s a Wrap

We have proven another interesting property of the popcorn function. We know that $T$ continuous on irrational numbers and discontinuous on the rational and now we know that it’s Riemann integrable on any closed interval. There was enough information in the proof for you to be able to deduce $\int_0^1 T(x) \;dx,$ leave your answer in the comments!

I hope you had some fun today! Remember math is supposed to be fun!

Be Kind. Be Curious. Be Compassionate. Be Creative.

And Have Fun!

A Kick in the Discovery