The Pythagorean Theorem

The Pythagorean Theorem isn’t only one of the most useful theorems in mathematics, it’s also one of the most beautiful! There are also more than 350 different proofs out there for you to enjoy! Today, I wanted to cover one of the most famous, and I wanted to do it with minimal text. Let’s get going!

The Pythagorean Theorem: Let a right triangle’s two legs have length $a$ and $b$ as well as a hypotenuse with length $c.$ Then,

$a^2+b^2=c^2$

Proof: (Click in the Discovery)

Let’s draw a the right triangle described as well as implementing the trick where we interpret $a^2, b^2,$ and $c^2$ as areas of squares! We’ll draw those squares, so they align with the triangle’s sides,

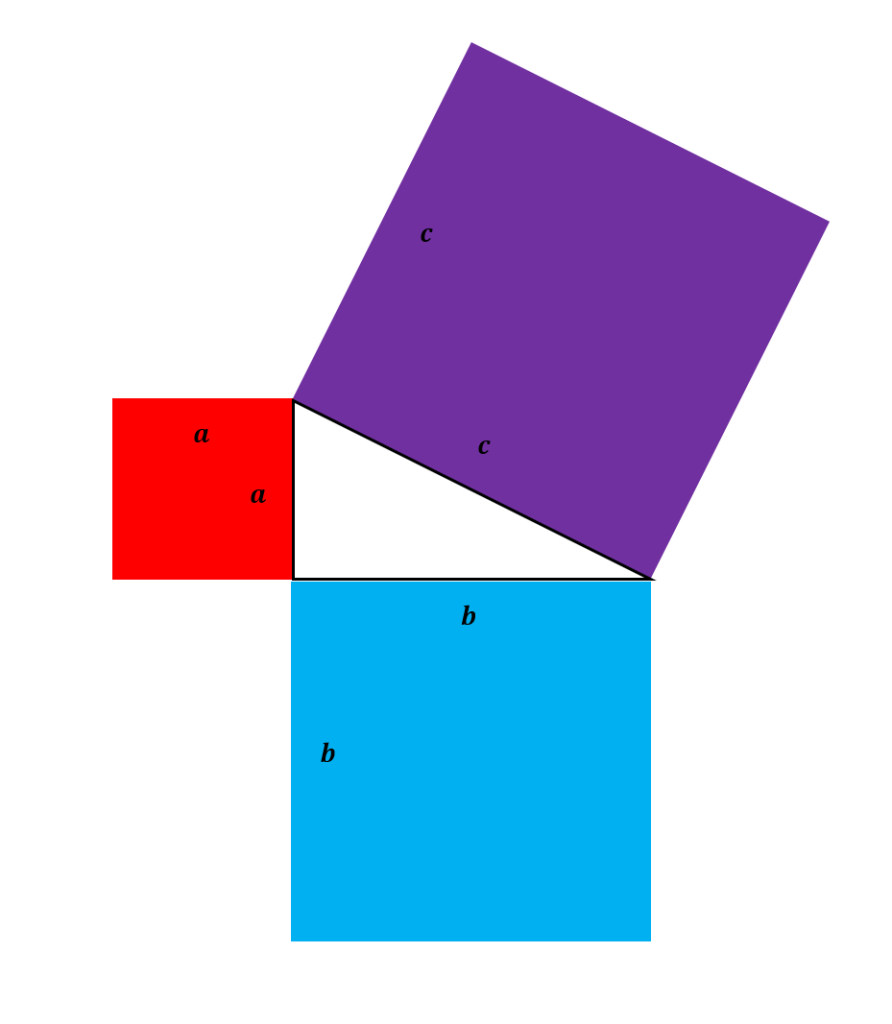
Our goal is to prove that the red area plus the blue area equal the purple area. I don’t want to give away the answer just yet, so take a moment to think of a way you can rearranlge the squares to make a larger square. Hint: you will need to use four triangles.

Click in the Discovery (AGAIN)

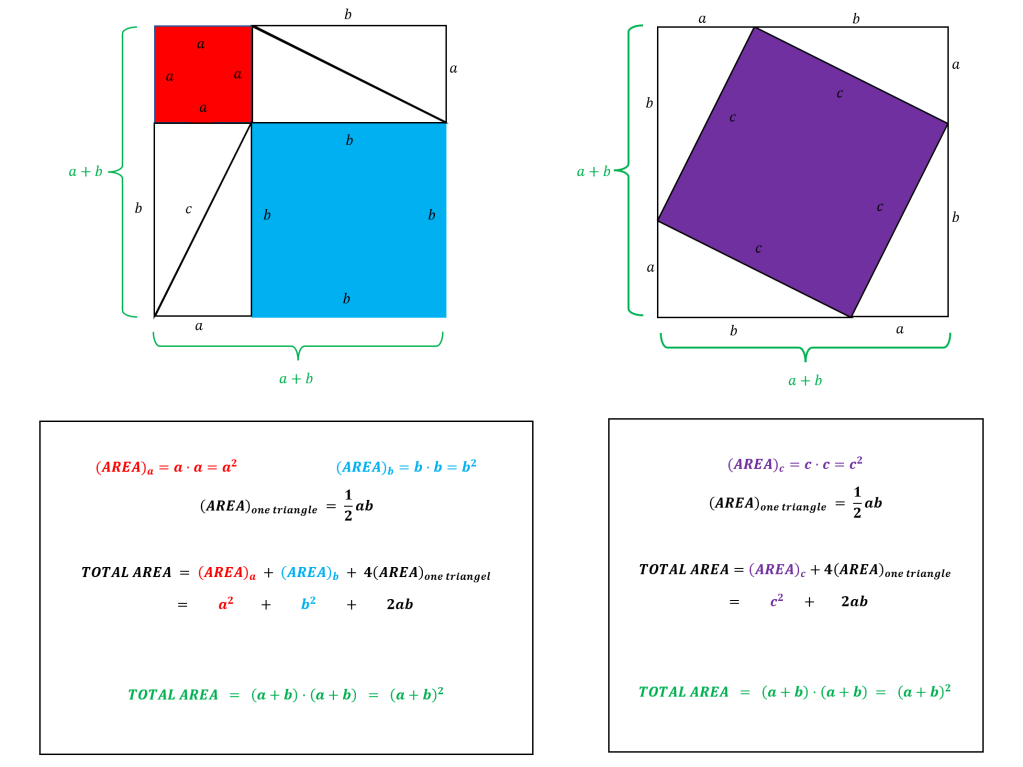
Note that we know that these puzzles made of squares and triangles are squares with side lengths $a+b$ because the right triangles have angles such that $\angle ac + \angle bc + 90^{\circ} = 180^{\circ}.$

$\square$

Short and Sweet

Today’s article was a lot shorter than the usual article, but I hope just as fun! I would like to make one final comment, it’s that this proof is not a full-on Proof. This is because we didn’t justify every step using the Axioms of geometry, or theorems proved that relied on the axioms. For example, how do we know we can construct squares with side lengths $a,b,$ and $c$ ? However, I’m sure you are comfortable with assuming that you can do this, and this is why this proof was good enough for us—or at least for me! It gives the spirit of the proof and the joy of how creative the proof is. With that said, you can check our Euclid’s rigorous proof in his Elements. It’s beautiful because of how carful and rigorous he is. But, for those who don’t want to read it, check out these lecture amazing lecture series,

Be Kind. Be Curious. Be Compassionate. Be Creative.

And Have Fun!

A Kick in the Discovery