Let’s Get Real… Analysis (Part 8): Superb Subsequence

Sometimes we have sequences that don’t converge, and yet, it’s possible to take elements from the divergent sequence to form a convergent sequence. We refer to such sequences as subsequences, which will be the topic of interest today. But you knew that, you saw the title of today’s article!

Also, we’re going to try a new format for these articles. We will be boxing definitions, lemmas, propositions, and theorems, in blue and the proofs will be in a red. Furthermore, the proofs will be in a pull-out menu, so that way if you want to try working out the proof you won’t accidently see it beforehand! Just click on, Click in the Discovery, to open the proof. Also, keeping the proof mildly hidden might help with those of you who don’t care about the proofs and want to read only the statements and not loose continuity of the article. Please let me know it you like these changes!

When Life Gives You a Sequence, Make a Subsequence

A subsequence is essentially what it sounds like. Even so, let’s formally state it

Definition (Subsequences): Let $(a_n)$ be a sequence. A subsequence of $(a_n)$ , denoted $(a_{n_k})$ , is a sequence obtained by taking elements from $(a_n)$ , while keeping them in the same order.

To be precise, let $(a_n)$ be a sequence of real numbers and let $(n_k)$ be a strictly increasing monotone sequence of natural numbers, i.e., $n_k <n_{k+1}$ and $n_k \in \mathbb{N}$ for all $k$ . Then, $(a_{n_k})$ is a subsequence of $(a_{n})$ .

The phrase, strictly increasing monotone sequence of natural numbers, means: $n_1<n_2<n_3<\cdots<n_k<\cdots$ for all elements of the sequence $(n_k)$ and that each of those elements are positive integers: $n_k \in \mathbb{N}.$ This is the condition that forces the subsequence’s elements to remain in the same order as they appear in the main sequence. For example, take the sequence $(a_n) = (n)$ ,

$(a_n) \;:\;1,2,3,4,5,6,\cdots$

Any of the following could be subsequences of $(n)$ ,

$1,3,6,8,9,10,\cdots \\ 1,2,3,4,5,6,7,\cdots \\ 2,4,6,8,10,12\cdots\\5,10,15,20,25,30,35,\cdots \\5,10,15,16,17,18,19,\cdots$

Some of those subsequences can be more easily expressed as,

$(a_{n})\;\;:\;1,2,3,4,5,6,7,\cdots \\ (a_{2k})\;:\;2,4,6,8,10,12,\cdots\\(a_{5k})\;:\;5,10,15,20,25,30,35,\cdots$

A non-example is $1,3,5,4,7,\cdots$ since $a_5 = 5$ occurred before $a_4 = 4$ .

A Property of Subsequences

Question: If we have a convergent sequence, say $a_n \rightarrow \alpha$ , then what would you guess about an arbitrary subsequence $(a_{n_k})$ of $(a_n)$ ? Do you think $a_{n_k} \rightarrow \alpha$ sometimes, always, never? If you answered: always, then congrats, because you’re correct, as the next proposition states.

Proposition: Let $(a_{n})$ be a sequence. If $a_n \rightarrow \alpha$ , then any subsequence of $(a_n)$ also converges to $\alpha$ . Conversely, if every subsequence of $(a_n)$ converges to $\alpha$ , then $a_n \rightarrow \alpha$ . In symbols,

$a_n \rightarrow \alpha \iff \forall a_{n_k} \rightarrow \alpha.$ .

Scratch Work:

Ok, so we want to show there is some $N \in \mathbb{N}$ such that,

$|a_{n_k} - \alpha| < \varepsilon$

for all $n_k>N.$ Right? Well, not quite… The elements of $(a_{n_k})$ are indexed by $k$ so we want to do is find a $N \in \mathbb{N},$ such that `blah blah blah’ for all $k>N$ . But as we will see, in the following lemma, there is a nice relationship between $n_k$ and $k.$ You may think it’s intuitive too: $n_k\geq k$ for all $k$ . Said in a more precise and mathematical way:

Lemma: Let $(n_k)$ be a strictly monotone increasing sequence of natural numbers. Then, $n_k\geq k$ for all $k\in \mathbb{N}$ .

Proof of Lemma: (Click in the Discovery)

Let $(n_k)$ be a strictly monotone increasing sequence of natural numbers. Then, $n_k\geq k$ for all $k\in \mathbb{N}$ .

Our base case is simply the statement: $n_1 \geq 1,$ which follows from the fact that $1$ is the smallest natural number (for those who are wrong thinking that $0\in \mathbb{N},$ no the number $0$ is a not natural number! haha). Now assume that $n_k\geq k$ for some $k\in \mathbb{N}$ and consider $n_{k+1}$ . Since $n_{k+1}>n_k\geq k$ , it follows that $n_{k+1}\geq n_k + 1 \geq k+1$ and boom! We’re done… by induction.

$\square_{\mathrm{Lemma}}$

Ok, can you try to use this to prove the proposition using the lemma before we tackle it together??? Go for it and don’t worry if you cannot figure it out. It’s the attempt that matters!

Proof of Proposition:

Proof of Proposition: (Click in the Discovery)

Let $(a_n)$ be a sequence of real numbers and let $(n_k)$ be a strictly monotone increasing sequence of natural numbers.

Forward: $a_n \rightarrow \alpha \implies \forall a_{n_k} \rightarrow \alpha$

Let $\varepsilon>0$ and $a_n \rightarrow \alpha$ . By definition, there is some $N \in \mathbb{N}$ such that,

$|a_{n} - \alpha| < \varepsilon$

for all $n>N$ . Consider a subsequence $(a_{n_k})$ of $(a_{n})$ . Using our lemma, when we have $k>N$ , we also have $n_k>N.$ Moreover, since the elements $a_{n_k}$ are taken from $a_n$ , the same value of $N$ works! That is, we have

$|a_{n_k} - \alpha| < \varepsilon$

for all $k>N$ .

Backward: $\forall a_{n_k} \rightarrow \alpha \implies a_n \rightarrow \alpha$ .

“For all” statements are usually hard to prove, in which case it’s sometimes beneficial to try to construct a proof by contradiction or a proof by contrapositive. We will work to prove the contrapositive:

If $a_n \nrightarrow \alpha$ , then there exists a subsequence $a_{n_k}$ such that $a_{n_k} \nrightarrow \alpha$ .

In symbols

$a_n \nrightarrow \alpha \implies \exists a_{n_k} \nrightarrow \alpha$

Okay, we are starting with the assumption that $a_n \nrightarrow \alpha$ . Therefore, we know it’s not true that,

False: for all 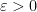$\varepsilon>0$ , there exist an 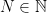$N \in \mathbb{N}$ such that $|a_n - \alpha| <\varepsilon$ for all $n>N$ .

In other words, it is true that:

True: there exists a 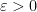$\varepsilon>0$ such that for all $N\in \mathbb{N}$ there exists a $n>N$ such that $|a_n - \alpha| \geq \varepsilon$ .

We will use the True statement to create a subsequence $(a_{n_k})$ that doesn’t converge to $\alpha$ .

First, let $n_{1} = 1,$ and hence $a_{n_1} = a_1$ .
Second, there is some $n_{2} \in \mathbb{N}$ such that $n_2>n_1$ and $|a_{n_2} - \alpha| \geq \varepsilon$ .
Next, there is some $n_{3} \in \mathbb{N}$ such that $n_3>n_2$ and $|a_{n_3} - \alpha| \geq \varepsilon$ .
Then, there is some $n_{4} \in \mathbb{N}$ such that $n_4>n_3$ and $|a_{n_4} - \alpha| \geq \varepsilon$ .
By continuing this process inductively, we construct a subsequence that doesn’t converge to $\alpha$ .

This concludes the proof of the proposition.

$\square_{\mathrm{Proposition}}$

This proposition is handy! It gives us a quick way to prove that sequences like $(-1)^n$ diverge through the contrapositive of the forward direction:

Contrapositive of Proposition: Let $(a_{n})$ be a sequence. If $a_n \nrightarrow \alpha$ , then there exists a subsequence of $(a_n)$ that doesn’t converges to $\alpha$ . Conversely, if there exists s subsequences of $(a_n)$ that does not converges to $\alpha$ , then $a_n \nrightarrow \alpha$ . In symbols,

$a_n \nrightarrow \alpha \iff \exists a_{n_k} \nrightarrow \alpha.$ .

For instance, compare the following proof to what we showed previously here in example 3.

The sequence $(-1)^n$ diverges.

Proof: Let $(a_n) = (-1)^n$ . First define $(n_k) = (2k)$ . We will construct two subsequences that converge to different limits.

(i) First, consider the subsequence of even-indexed elements from $(a_n)$ , that is: $(a_{2k}) = (-1)^{2k} = 1$ . Note that, $(a_{2k}) \rightarrow 1$ .

(ii) Next, consider the subsequence of odd-indexed elements from $(a_n)$ , that is: $(a_{n_k})=(a_{2k+1}) = (-1)^{2k+1} = -1$ . Note that, $(a_{2k+1}) \rightarrow -1$ .

Finally, since we found the two subsequences $(a_{2k})$ and $(a_{2k+1})$ of $(a_{n})$ that converge to two different limits, we conclude that $(a_{n})$ does not converge.

$\square$

Are you still reading this?

You may wonder why we care about subsequences in the first place. If so, then good! You’re a critical thinker and that’s appreciated. Unfortunately, I’m only going to give you an unsatisfying answer in the form of a quote from my real analysis professor: “There are many things that you just cannot do without working with subsequences.” Enough said. But if that wasn’t enough (which it’s probably not enough) then you’ll be happy to hear that the week after next week we will discuss the always amazing Bolzano-Weierstrass Theorem! (Love that theorem sooooo much!) Which relies on subsequences.

Before we finish, the last thing that should be mentioned is that everything that we have been talking about in our Let’s Get Real… Analysis series regarding sequences also holds for subsequences. This is because subsequences are sequences too!

Be Kind. Be Curious. Be Compassionate. Be Creative.

And Have Fun!

A Kick in the Discovery

Let’s Get Real… Analysis (Part 8): Superb Subsequence