A Kick in the Discovery

Last week we learned some tricks to derive some trigonometry identities quickly while using Euler’s formula; however, once I finished writing it, I wanted to prove the same rules using triangles and geometry! I thought it would be fun and boy howdy was I right!

Back in school I disliked geometry for some reason, I think I just didn’t appreciate the idea of proof writing in that style. Once I learned general relativity and that gravity is basically the geometry of spacetime, I became very enthusiastic towards geometric arguments. So, in an effort to give myself something fun to play with, let’s find the sum of angles formula: .

A word of caution, geometry arguments can be particularly difficult to follow. Usually this is due to figures becoming overly cluttered. So, I recommend you try to derive the formula on your own, and if you need to, use this article as only a check or motivation for what to do next.

Here We GOOOOOO!!!

GOAL:

To begin. let’s draw a unit circle with a right triangle with an angle as shown below.

Great! Now add a triangle with angle on top.

We can also draw in a right triangle with angle , but this time the leg that would usually be drawn on the x-axis will be on the hypotenuse of the blue triangle.

Where we got rid of the purple triangle so that we could declutter the image. Let’s put the purple triangle with angle back in using dotted lines for its legs.

Notice how the base is what we want to compute. Our goal reduces to being able to find this length in terms of

Take a look at the red triangle. There is a little right triangle that is made using the smallest red leg and the dotted purple line.

Do we know anything about the angles of the green triangle? Take a moment to ponder this and then scroll to the next photo in the above gallery.

Keep thinking!

The green triangle is similar to the blue triangle! It’s more obvious when you label the angle complementary to in the blue and green triangles (since they are vertical angles).

Let’s try to find the hypotenuse of the green triangle. We’ll denote the length by . Remember that the leg that overlaps with the red triangle has length , and now using the angle from the green triangle we also have the following:

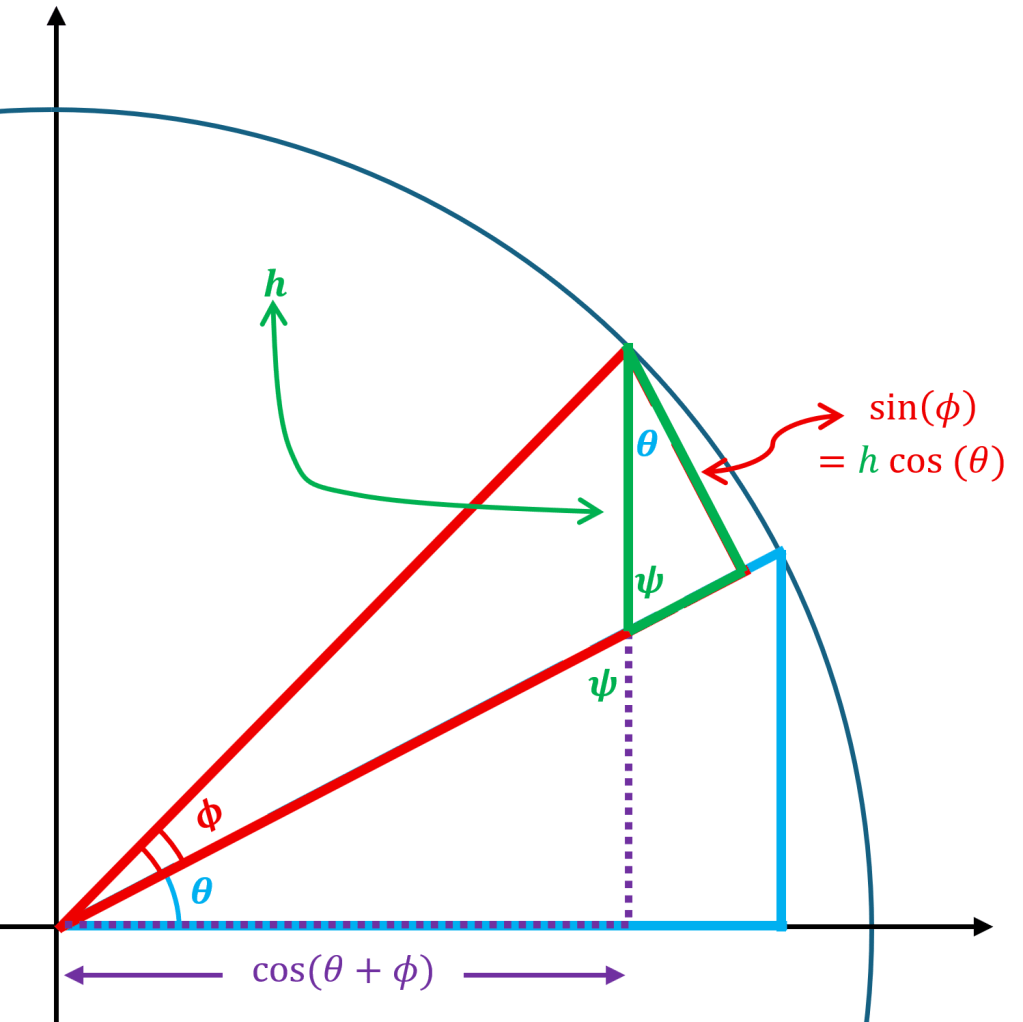
We can solve for using the two expressions for the length of the overlapping green and red leg:

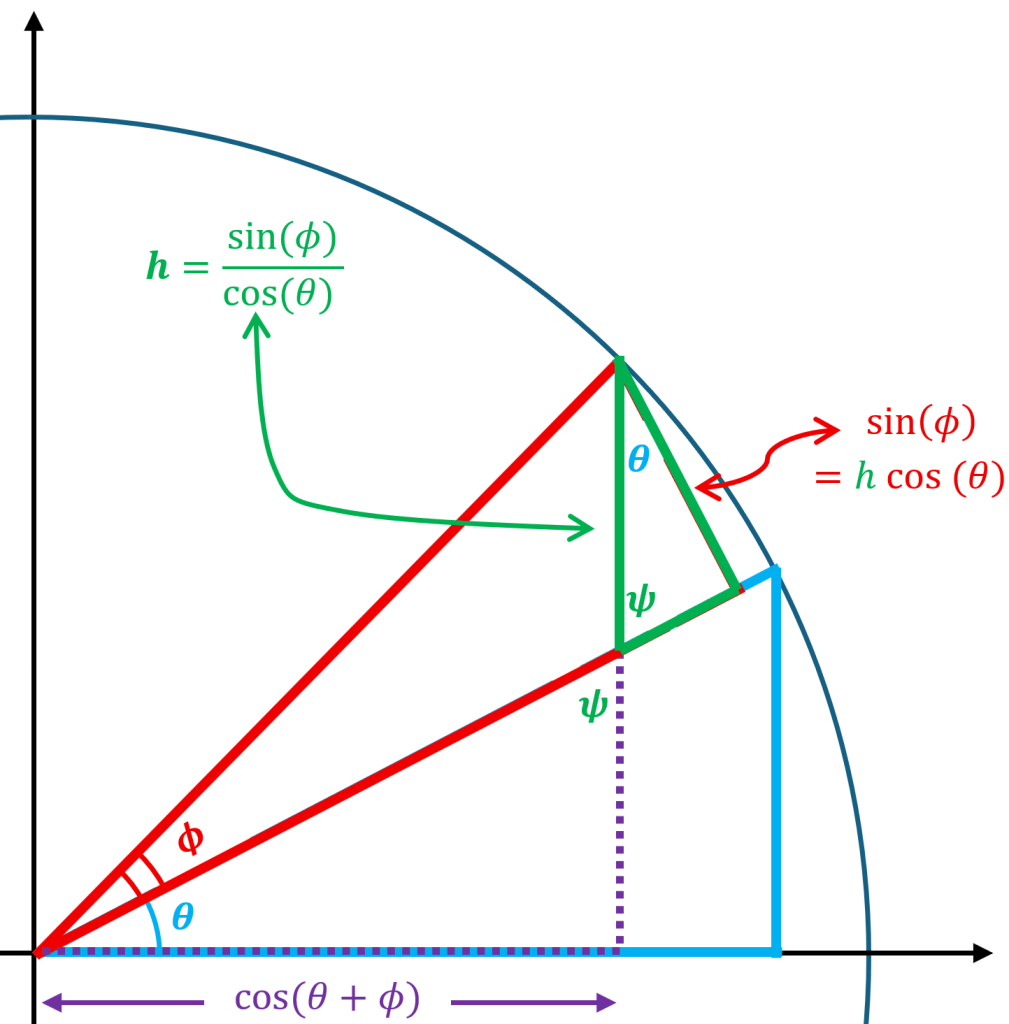
We know two out of the three sides of the green triangle, but it turns out that the one we need is the last leg that we haven’t found. We color it yellow below,

Ok, let’s keep going! We are on a rollllllll!!!!!

We can use this yellow line to form another right triangle similar to the blue triangle! Take a look:

Let’s find the bottom leg of this yellow triangle now. We know the hypotenuse, and so we deduce the bottom leg will be times the length of the hypotenuse:

Almost there!

Let’s get rid of almost everything we’ve done so far except for the blue and red triangles. We know that the bottom leg of the red triangle has length . By using the bottom leg of the right triangle, we can form yet another triangle similar to the blue one. This time the bottom leg of the similar triangle is given by .

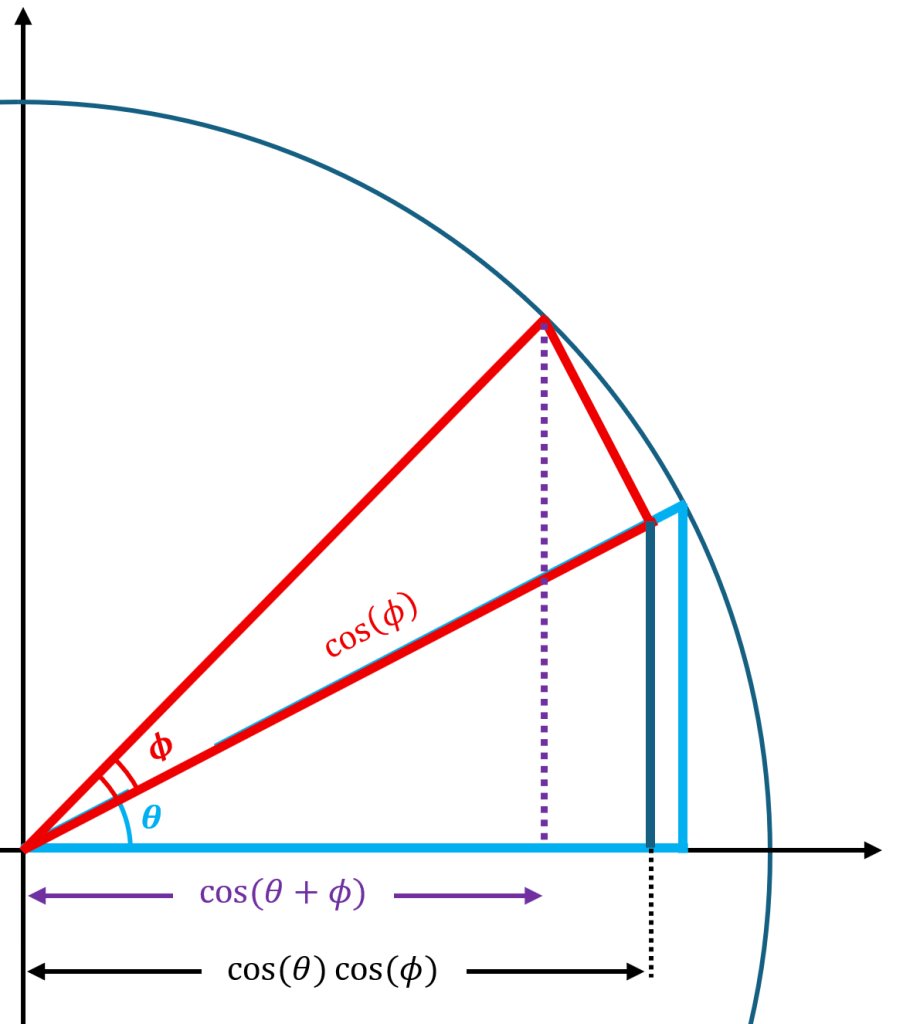
Putting back some information, we see the following segmentation of the bottom leg:

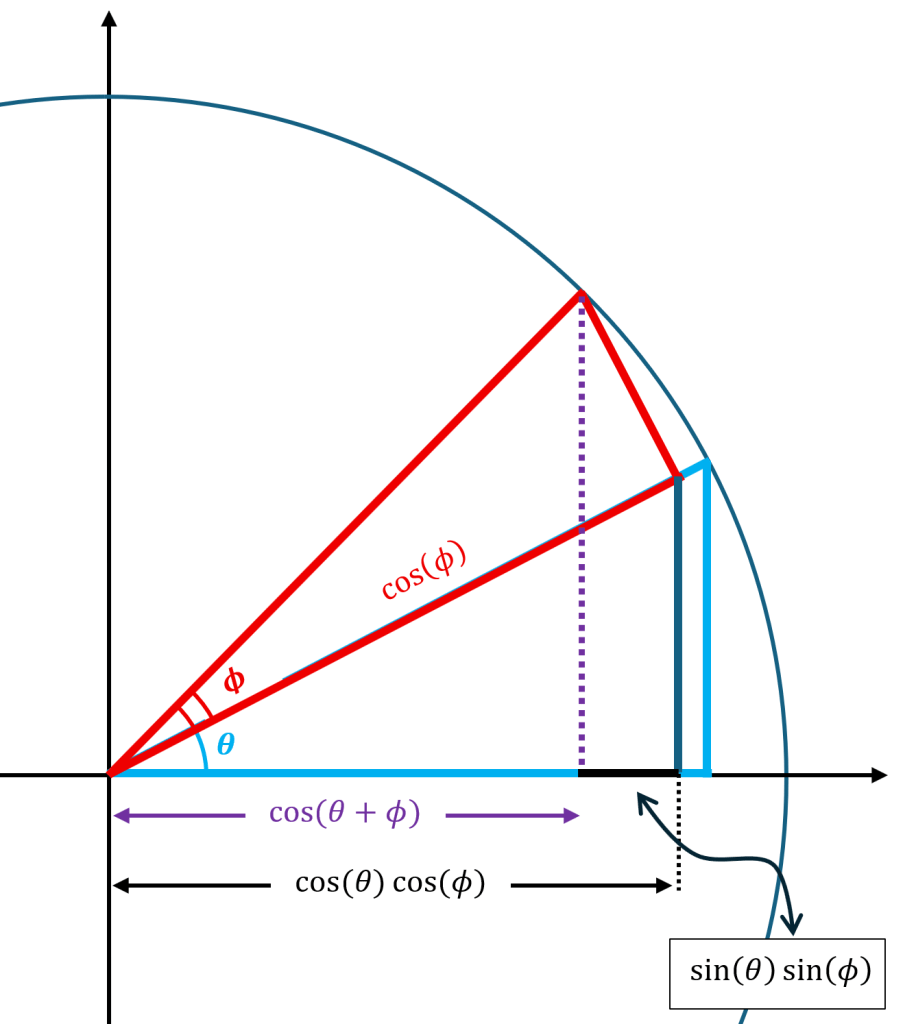
Thus, we find,

,

and hence,

And we are done!

Ooofff that was a lot… of fun!

Geometry Is FUN

Although I admit that geometry is not always the most fun activity in the world, I hope that you give it a chance. The great thing about geometry is that it requires very little advanced mathematics. All you really need is to be clever, and for this reason I think it has the potential to be the most fun math that you get to do in high school!

I hope that you gave this an effort and did not just read through (or look through) what I came up with. Oh, and if you did it a different way than me send it over! Or put it in the comments! I am more than happy to learn more ways to carry out this derivation.

As a challenge can you prove that the following geometrically:

I hope you get a kick in the discovery while trying it out!