What Comes Next: 1, 2, 4, 8, 16, … hint it’s not 32

A Kick in the Discovery

, ,

Time Dilation Through the Geometry of Right Triangles

Published by

Valt

on

Today’s an exciting day, our first venture into physics together. Since everyone, including myself, loves time dilation and special relativity I really wanted to start with this topic. Also, a small comment one of my friends made regarding how crucial geometry was to the development of modern math and science gave me this perspective to take for this article.

Yet another reason why I wrote this is that most people don’t know how easy (compared to general relativity) it is to derive the equation that describes time dilation between two observers. This is our humble goal for today. Discover for ourselves what Einstein discovered back in 1905.

Thought Experiment

Photo from nobelprize.org

Einstein was a master of coming up with thought experiments in order to motivate his theories. We are going to set up our own! But before we do, let’s talk about what our endgame is.

You may have heard that, someone moving with respect to you will have their time run more slowly than your time. Indeed, this is true, and it’s just one of the things that Einstein taught us. We want to go one step further though; we want to try to quantify this phrase `slowing down time’. In order to do so, we will have two scientists Mae and Albert. Mae is a brave astronaut and will be the one moving with respect to the physicist Albert on the ground.

Mae will be in the moving reference frame of a rocket and Albert will be stationary and will be observing Mae. We must come up with a way to measure how much time passes for Mae in the ship and Albert on the ground. Once we do, we will compare them, and this comparison will lead us to the famous time-dilation equation of special relativity.

Enough stalling on my part, let’s get into it!

Astronaut Mae’s Time Keeping Problem

Imagine, if you will, an astronaut named Mae in a rocket ship traveling at a constant speed of v above Earth. Mae wants to set up a way to measure her time so that we and Albert can compare our time to hers.

Let’s help Mae come up with some ideas.

Idea 1: Don’t over think, just use a stopwatch. My first guess would be to just use a very precise stopwatch to measure how much time elapses. However, how would we compare this measurement to one that Albert is making on the sidelines? We know that one stopwatch should run slower than the other, but there is no obvious way to quantify how much they will disagree if we only use a standard stopwatch/clock on the ship.

Idea 2: Don’t have a clock on the ship. Well, since any standard time measuring devise Mae uses will start to run slowly because of time-dilation, maybe we should put a clock outside the ship on the ground with Albert. Then Mae can watch the clock on the ground. However, this runs into the same issue as the previous idea, there is no obvious way to determine how much their relative time changes because Mae has nothing standard to compare her time to!

Maybe that’s it! We need something that doesn’t change for Mae and Albert so that way we can make a meaningful comparison. What is something that is constant for everyone?

Idea 3: Use something that does not change for both Mae and Albert as a clock. Since the issues with ideas 1 and 2 come from the fact that there is no easy way to compare their standard clocks (they both have their own internal gears/mechanisms) we decide to make a clock using something universal: light. Einstein taught us in his theory of special relativity that the speed of light is constant for every observer (that isn’t accelerating). This makes light the perfect tool to use to measure elapsed time for both Mae and Albert.

With the idea of using light and in a feet of ingenuity Mae makes herself a light-clock. She uses a laser and two reflective surfaces. First, Mae sets the surfaces up to have a vertical distance of h meters between them (h for height). Next, she sends a laser pulse between them in such a way that one laser pulse will reflect back and forth between the two surfaces. See the figure below.

Mae is in her rocket ship. She has set up her light-clock so that light will bounce up and down between the two reflective surfaces in blue. The lights path is marked by the yellow arrows.

Mae quantifies how much time passes by counting how many times the light hits the bottom surface. So, she is using the time it takes for the light to make one full journey up and down as her measurement standard. Since she knows both the speed of light, denoted c, is equal to 299,792,458 meters per second and how far apart the surfaces are, h meters, she can use some math(s) to determine how much time has passed by counting how many oscillations that light goes through!

Let’s do some of this math(s) that Mae did.

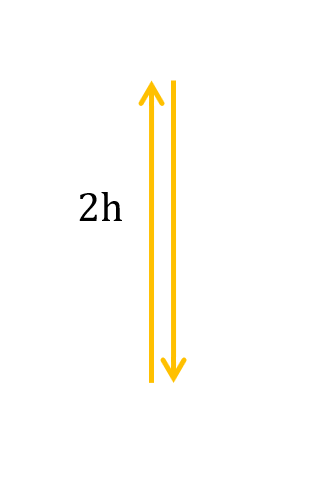
The distance between the two reflective surfaces is equal to h, therefore the light would travel a distance of 2h in order to make it back to where it started:

Mae then used that speed = \frac{distance\;traveled}{elspsed\;time}, in order to calculate that the time elapsed for one of these oscillations is,

\boxed{t_{m} = \frac{2h}{c}}.

Where we have t_m denoting how much time Mae would measure.

We will soon find it is useful to rewrite the above relationship in the following way,

\boxed{2h = ct_{m}}.

Just like that we’re momentarily done with Mae’s perspective; she’s already done enough work making that light clock! Let’s continue by changing our perspective to Albert’s who’s watching Mae in her rocket.

Albert’s Perspective on the Ground

We now join our second scientist, Albert, on the ground who’s watching Mae as she flies over head at a constant speed v.

Albert is curious how well Mae’s light clock will work. He also wants to use her clock to measure how much time elapses and compare it to what Mae would say. Just like Mae, Albert is one smart cookie and notices that the light beam must trace out a triangular path as it oscillates in, and moves forward with, the ship. We draw this path using the yellow arrows below:

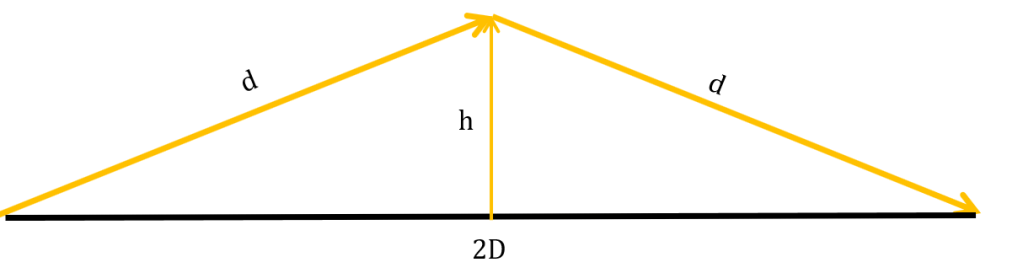
If we can find out how far the light travels, we can use the speed of light to determine how much time elapsed. So, Albert sets out to determine how long the yellow sides are. Mae told him that the height of the light-clock is h. Therefore, the height of the triangle is h. Albert adds this information to his drawing of the triangle. But he also notices that the bottom (black side) is equal to the distance Mae travels in the time interval that we are trying to measure. Albert calls this distance 2D.

Albert does not like obtuse triangles, so he cuts the triangle in half to make it a right triangle, which he loves.

Albert knows a little physics and brings that in to help. First, Albert knows that Mae is traveling at a speed of v meters per second, therefore the amount of time Albert measures for how long it takes Mae to travel a distance of 2D (denoted t_{a}) is found in the following way,

v = \frac{2D}{t_a}\implies t_{a} = \frac{2D}{v}.

He also knows that it will be more convenient to have this relationship in terms of D,

D = \frac{vt_{a}}{2}.

WARNING, WARNING PRACTICAL USE OF THE PYTHAGOREAN THEOREM ALERT!

Albert then uses the Pythagorean theorem to deduce that the distance the light travels is,

d^2 = h^2 + D^2 = h^2 + (\frac{vt_{a}}{2})^2.

Recall that Albert also knows that the speed of light is always c, so he says that c = \frac{2d}{t_{a}} since the light travels a distance 2d in an amount of time t_{a}. Using this in the above equation we get,

(2d)^2 = (2h)^2 + (vt_{a})^2.

\implies\boxed{(ct_{a})^2 = (2h)^2 + (vt_{a})^2}\qquad \textit{ }\qquad

Bringing it All Together

It might surprise you that we are almost done! We don’t need Mae or Albert’s help anymore; all we need to do is use our boxed results to bring Mae’s time measurement and Albert’s time measurement together.

Let’s use the equation Albert just found and plug it into what Mae found. As a reminder she found, 2h= ct_{m}. Thus,

(ct_{a})^2 = (2h)^2 + (vt_{a})^2 \\ \textit{ }\qquad\, = (ct_{m})^2+ (vt_{a})^2

Let’s divide both sides by (ct_{a})^2, and then carry out some algebra,

1 = \frac{(ct_{m})^2}{(ct_{a})^2}+ \frac{(vt_{a})^2}{(ct_{a})^2} \\ \textit{ } \,=\left(\frac{t_{m}}{t_{a}}\right)^2+ \left(\frac{v}{c}\right)^2

All we have to do is solve for Albert’s time to get

\boxed{t_{a} = \frac{t_{m}}{\sqrt{1- \frac{v^2}{c^2}}}}.

This is the famous time dilation equation! Let’s change some of the letters to make it look more standard.

We’ll denote Albert’s time by \Delta t where the triangle before the t means change in time. We will then change Mae’s time for the Greek letters \Delta \tau which mean change in proper time. Where proper time is the fancy sounding term we give to the time measured in one’s own resting frame. And since Mae is not moving with respect to her light-clock, she would be measuring her proper time.

With these changes we get,

\boxed{\Delta t = \frac{\Delta \tau}{\sqrt{1- \frac{v^2}{c^2}}}}.

Much nicer looking huh? 1

What do we Learn from this Equation???

This equation is all well and good, but what can we learn from it? A great first pass at understanding the time-dilation equation can be found by plugging in a value for Mae’s time \Delta \tau , and some different values for Mae’s speed v. To keep things simple, let’s say that Mae measured only 1 second so that her proper time is \Delta \tau = 1 second. Now let’s see how the time Albert would measure \Delta t changes as Mae speeds up!

Mae’s speed vAlbert’s Measured time \Delta t Mae’s Time \Delta \tau
100 miles per hour
(= 44 . 704 meters per second)		1 . 000 000 000 000 011 1 seconds1 second
Mach 1 (the speed of sound)
(=342 . 9999338 meters per second)		1 . 000 000 000 000 655 seconds1 second
The Speed of the ISS
7 , 660 . 477 meters per second		1 . 000 000 000 326 seconds1 second
Parker Solar Probe (the fastest human made object)
192 , 227 . 2 meters per second		1 . 000 000 206 seconds1 second
1 , 000 , 000 miles per hour1 . 000 001 11 seconds1 second
580 , 771 , 037 . 26736 miles per hour2 . 000 seconds1 second

Take a look at how fast Mae would need to go in order for Albert to experience 2 seconds for every 1 second of Mae’s! Even the astronauts on the ISS will only have their time dilated by 3\times 10^{-8} percent. *This is one of the reasons why no one noticed this phenomenon until Einstein! It’s also incredible that Einstein discovered it in the first place!*

Observe that the faster Mae moves, with respect to Albert, the more her time slows down compared to Albert. If Mae was moving at about 580,771,037 miles per hour for one year, then Albert would have lived two years. Mae is ageing and thinking more slowly than Albert!

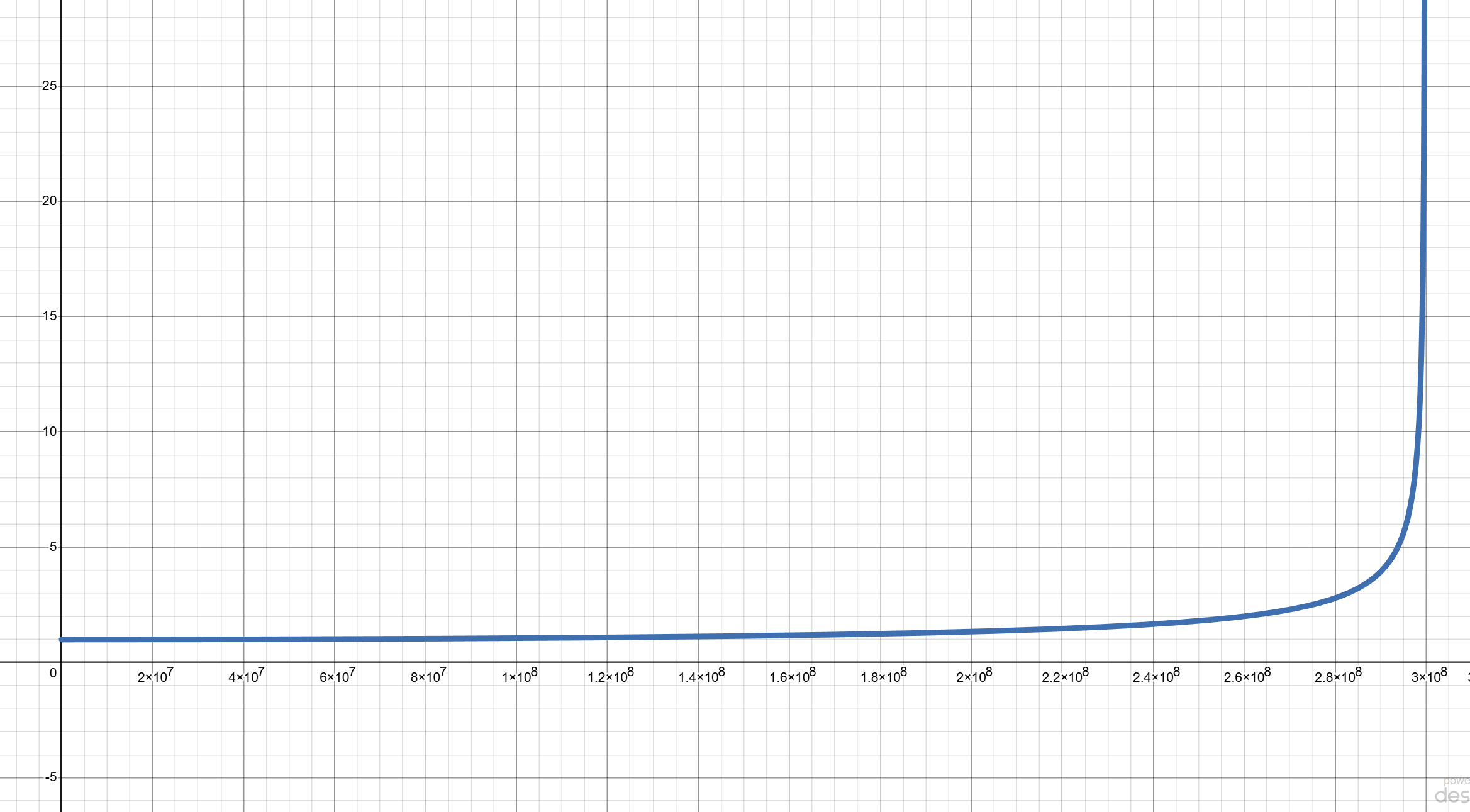
Let’s go one step better and graph this equation. Again, we will set Mae’s measured time to \Delta \tau = 1 second and we let Mae’s speed be the x-axis in meters per second. The y-axis will be what the time that Albert measures.

(Figure above): The x-axis is Mae’s speed in meters per second and the y-axis is the amount of time that Albert experiences for every 1 of Mae’s seconds.

By looking at the graph we now have added a layer to our knowledge, there is a sharp increase when Mae gets close to the speed of light. Take a look at the time-dilation equation again,

\Delta t = \frac{\Delta \tau}{\sqrt{1- \frac{v^2}{c^2}}}.

When Mae’s speed v gets closer to c the fraction \frac{v^2}{c^2} gets closer to 1. If Mae could travel at the speed of light, then v=c and \frac{v^2}{c^2} = 1. But then we’d divide by zero, which I’m sure you remember is frowned upon. This tells us something deep.

Nothing can travel faster than the speed of light, for some reason.

Wow how amazing!

One quick philosophical point regarding this speed limit. Some people have said that, since photons travel at the speed of light, they don’t experience time. Although the first statement is correct, the second statement is misleading. In my opinion, and this is my opinion because this is a nonscientific matter, we should be careful to anthropomorphize light. But, if you want to think of light as not having an internal clock, then go for it! It is mind blowing!

Now, all this effort we have put in means nothing if we cannot experimentally verify what we have found.

Experimental Evidence

The principle of science, the definition, almost, is the following: The test of all knowledge is experiment. Experiment is the sole judge of scientific truth. – Richard Feynman

There is far too much evidence to go over in one article, and this article is long enough as it is. But we wouldn’t be doing science if we did not even mention any of the ways that time-dilation has been experimentally verified. We will not give all the details, but there will be a few links for you to check out them if you are interested.

Enter, the humble muon (a subatomic particle). There are what we call cosmic rays that, when passing through the Earth’s atmosphere, will produce muons. These muons have a very short half-life (if you haven’t heard of half-life think of it as a measure for how long the muon lives before it decays). Their half-life is so short that we’d expect them to not be able to reach us on the surface of the Earth because they’d decay before they got here. In fact, if they did, we might have naïvely said they were traveling faster than the speed of light in order to reach us in time!

But, when we look for them, we find them! They somehow reach us even though they shouldn’t. The reason they do, is because they are traveling so fast their time dilates and they feel less time than you’d expect before Einstein. Moral: Their proper time slows down so much that their short half-life from our perspective is long enough to make it to Earth’s surface.

How awesome is that!

Somehow Einsteins relativity knows about radioactive decay, which is a nuclear process. It’s absolutely incredible how far-reaching physical theories can be!

Concluding Remarks

I hope you enjoyed a little Einsteinian relativity today! I’m going to leave, as a challenge, the derivation of length contraction. Just as time dilated for Mae, her length would contract in the direction of motion. The idea is the exact same, come up with a way to measure lengths using light, and then compare what Mae and Albert would deduce. I hope you get a kick in the discovery with the challenge!

Let me know how it goes in the comments! Until next (proper) time!

Sources for muon decay:

Footnote:

  1. If we want to go nuts, we might introduce the Greek letter \gamma to symbolize \frac{1}{\sqrt{1- \frac{v^2}{c^2}}}, ie \gamma = \frac{1}{\sqrt{1- \frac{v^2}{c^2}}}. This makes the time dilation equation seem much nicer,
    \Delta t = \Delta \tau \cdot \gamma.
    But unless you know what \gamma means it loses some meaning. ↩︎

Leave a comment