What Comes Next: 1, 2, 4, 8, 16, … hint it’s not 32

A Kick in the Discovery

, ,

It’s Pi Day!

Published by

Valt

on

For the first Pi day after having started akickinthediscovery.com I figured that we should do something special! We’re going to show that the sum of the reciprocals of the squares equals… a surprise alla Euler:

\sum_{n=1}^{\infty}\frac{1}{n^2}= a surprise.

*******Tangent: We call numbers like 2^2, 3^2, 10^2, n^2 square numbers because they are the area of a square with side lengths 2, 3, 10, n respectively. Tangent over.*******

There is a wonderful history to this problem (the sum of the reciprocals of the squares) and I can in no way describe it better than the math historians out there, so I defer the history to the historians! But, just in case you don’t want to leave this page, long story short no one could solve this problem for a long time. Everyone wanted to know what this sum converged to (the limit version of equaling), but no one, not even the greats like Newton and Leibniz could do it. Not until Euler at only 28 years old, who was unknown at the time, came along and showed the sum of the reciprocals of the squares equals an utterly surprising value. He ended up proving this in a few ways, however, I’d like to prove it in my favorite of his methods. I’d like to give much thanks to William Dunham and Stony Brook University for teaching me this proof!

Theorem: (Euler) The sum of the reciprocals of the squares equals a surprise:

\sum_{n=1}^{\infty}\frac{1}{n^2}= a surprise!

****Note: Euler did not have rigorous analysis so some of these steps would need more through justification than he gave, and therefore what I give.****

Here’s some music to listen to while you read this wonderful proof!

Proof: To begin we will write the sine function as an infinite product. How might we go about this? Well, we know that the zeros of sine are any of the integer multiples of \pi namely: 0,\pi,-\pi,2\pi,-2\pi,\cdots, n\pi,\cdots. Recall that when we have a polynomial with zeros at say 0,\pi,-\pi then we would write the function as (note we could have an x^2 and not an x, so this process needs more finesse)

cx \left( 1 - \frac{x}{\pi} \right)\left( 1 + \frac{x}{\pi} \right) =cx \left( 1 - \frac{x^2}{\pi^2} \right)

*Where we used the fact that (a-b)(a+b)=a^2 - b^2.* Since sine has infinitely many zeros, we should be able to write it in the following way:

\sin{x} = c x \left( 1 - \frac{x}{\pi} \right)\left( 1 + \frac{x}{\pi} \right)\left( 1 - \frac{x}{2\pi} \right)\left( 1 + \frac{x}{2\pi} \right)\cdots \\\textit{ }\;\;\;\;\;\,=c x \left( 1 - \frac{x^2}{\pi^2} \right)\left( 1 - \frac{x^2}{4\pi^2} \right)\left( 1 - \frac{x^2}{9\pi^2} \right)\cdots

Where we choose c so that we have \sin{\pi/2}=1, in this case, c=1. For those who are skeptical about this, which you should be, we can check different values of x and see if they give the same result. This is what it seems like Euler did. Today, we would just graph the function and see what happens, check out this footnote for more.1 *Note this is one step that would need more rigor today*

Moral, we have the following infinite product for sine

\sin{x} = x \left( 1 - \frac{x^2}{\pi^2} \right)\left( 1 - \frac{x^2}{4\pi^2} \right)\left( 1 - \frac{x^2}{9\pi^2} \right)\cdots

Now let’s’ make our first, of many, substitution x=\pi y:

\sin{\pi y} =\pi y (1-y^2)\left(\frac{4-y^2}{4}\right)\left(\frac{9-y^2}{9}\right)\cdots

Since we are working with a product, yuck, we take some natural logs of both sides to get a sum,

\ln{(\sin{\pi y})} =\ln{(\pi)}+ \ln{(y)}+ \ln{(1-y^2)}+\ln{\left(\frac{4-y^2}{4}\right)}+\ln{\left(\frac{9-y^2}{9}\right)}\cdots \\\textit{ }\qquad\qquad=\ln{(\pi)}+ \ln{(y)}+ \ln{(1-y^2)}+\ln{\left(4-y^2\right)}-\ln{(4)} + \ln{\left(9-y^2\right)}\\\textit{ }\qquad\qquad\;\;\;\;\;\;\;\;- \ln{(9)}+\cdots

The problem is that we now have a bunch of logs that make things more difficult. To get rid of this we take the derivative with respect to y,

\frac{d}{dy}\ln{(\sin{\pi y})} = \pi\frac{\cos{\pi y}}{\sin{\pi y}}= \frac{1}{y} - \left(\frac{2y}{1-y^2}\right)- \left(\frac{2y}{4-y^2}\right)- \left(\frac{2y}{9-y^2}\right)- \left(\frac{2y}{16-y^2}\right)\cdots

With a little rearranging,

\frac{1}{2y^2} -\pi\frac{\cos{\pi y}}{2y\sin{\pi y}}= \left(\frac{1}{1-y^2}\right)+\left(\frac{1}{4-y^2}\right)+ \left(\frac{1}{9-y^2}\right)+ \left(\frac{1}{16-y^2}\right)\cdots

Now Euler tells us to make another (and more complex haha math pun) substitution: y = iz where i is the imaginary number \sqrt{-1}.

*Cue the thought: Where on Earth is Euler going with this argument?*

With this substitution we get:

\frac{-1}{2z^2} + \frac{\pi \cos{(-i \pi z)}}{2iz\sin{(-i\pi z)}} = \frac{1}{1+z^2} +\frac{1}{4+z^2}+\frac{1}{9+z^2}+\frac{1}{16+z^2}

Now we use Euler’s identity: e^{it} = \cos{(t)}+i\sin{(t)} to rewrite cosine and sine as,

\cos{(t)} = \frac{e^{it}+e^{-it}}{2} \qquad \mathrm{and}\qquad \sin{(t)}= \frac{e^{it}-e^{-it}}{2i}

Which we promptly use to simplify the left hand side \frac{\pi \cos{(-i \pi z)}}{2ix\sin{(-i\pi z)}} to be:

\frac{\pi \cos{(-i \pi z)}}{2iz\sin{(-i\pi z)}} = \frac{\pi \left(\frac{e^{\pi z}+e^{-\pi z}}{2}\right)}{ 2iz\left(\frac{e^{\pi z}-e^{-\pi z}}{2i}\right)} \\ \\ \textit{ }\qquad\qquad\, = \frac{\pi\left(e^{\pi z}+e^{-\pi z}\right)}{2 z\left(e^{\pi z}-e^{-\pi z}\right)}\\ \\ \textit{ }\qquad\qquad\,= \frac{\pi\left(e^{2\pi z}+1\right)}{ 2z\left(e^{2\pi z}-1\right)}

Now is where this gets messy! We will use what we just found and combine it with \frac{-1}{2z^2} to get,

\frac{-1}{2z^2} +\frac{\pi\left(e^{2\pi z}+1\right)}{2 z\left(e^{2\pi z}-1\right)} = \frac{-\left(e^{2\pi z}-1\right)+ \pi z\left(e^{2\pi z}+1\right)}{ 2z^2\left(e^{2\pi z}-1\right)} = \frac{-e^{2\pi z}+1+ \pi ze^{2\pi z}+\pi z}{ 2z^2e^{2\pi z}-2z^2}.

But let’s not lose track of the infinite sum we have this equal to:

\frac{-e^{2\pi z}+1+ \pi ze^{2\pi z}+\pi z}{ 2z^2e^{2\pi z}-2z^2}= \frac{1}{1+z^2} +\frac{1}{4+z^2}+\frac{1}{9+z^2}+\frac{1}{16+z^2}+\cdots,

and recall that the whole goal of this was to find the sum of the reciprocals of the square nummm…berrr…sss wait just a moment!!! Take a look at the right-hand side of the above equation, if we let z=0 then we have just what we wanted! Ok let’s do that set z=0 and we then get,

\frac{-e^{0}+1+ 0+0}{ 0-0}=\frac{0}{ 0}= 1 +\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\cdots

Aweeeeee we’re so close! But can we do anything with 0/0? For those who have taken calculus here’s a practical use of L’Hôpital’s rule! Remember, it’s that rule you thought you’d never use! For a reminder it tells us that:

L’Hôpital’s rule (applied to our situation):We ended up with f(z)/g(z) = 0/0 when we let z = 0. By taking the derivative of the numerator and denominator with respect to z the resulting rational function will have the same limiting value at z = 0.

So we just need to differentiate the numerator and denominator of \frac{-e^{2\pi z}+1+ \pi ze^{2\pi z}+\pi z}{ 2z^2e^{2\pi z}-2z^2} . This isn’t too bad, we get:

\frac{ \frac{d}{dz} \left( -e^{2\pi z} + 1 + \pi z e^{2 \pi z} + \pi z \right)}{ \frac{d}{dz} \left( 2z^2 e^{2\pi z} - 2 z^2 \right) }=\frac{ -2\pi e^{2 \pi z} + \pi e^{2\pi z} + 2 {\pi}^2 z e^{2\pi z} + \pi }{4 z e^{2\pi z} + 4 \pi z^2 e^{2\pi z} - 4z}= \frac{ -\pi e^{2 \pi z} + 2 \pi^2 z e^{2\pi z} + \pi }{4 z e^{2\pi z} + 4 \pi z^2 e^{2\pi z} - 4z}

We’re finally done, let’s plug in z=0 to see that the sum equals,

\frac{ -\pi e^{2 \pi 0} + 0 + \pi }{0 - 0} = \frac{0}{0}

Oh not again! I thought we were done… I guess we will use L’Hôpital’s rule a second time… hmmm… I don’t like this, it reminds me of calculus homework (this proof was actually in Euler’s Calculus textbook)! But we carry on

\frac{\frac{d}{dz}\left( -\pi e^{2 \pi z} + 2 \pi^2 z e^{2\pi z} + \pi \right)}{\frac{d}{dz}\left(4 z e^{2\pi z} + 4 \pi z^2 e^{2\pi z} - 4z\right)} = \frac{ -2\pi^2 e^{2 \pi z} + 2 \pi^2 e^{2\pi z} + 4 \pi^3 z e^{2\pi z} }{4 e^{2\pi z} +8\pi z e^{2\pi z}+ 8 \pi z e^{2\pi z}+ 8 \pi^2 z^2 e^{2\pi z} - 4} \\ \textit{ }\;\qquad\qquad\qquad\qquad = \frac{ \pi^3 z e^{2\pi z} }{e^{2\pi z} +4\pi z e^{2\pi z}+ 2\pi^2 z^2 e^{2\pi z} - 1} \\ \textit{ }\;\qquad\qquad\qquad\qquad = \frac{ \pi^3 z }{1+ 4\pi z + 2\pi^2 z^2 - e^{-2\pi z}}

We’re finally done (Déjà vu), let’s plug in z=0 to see that the sum equals,

\frac{ 0 }{ 1+0+ 0 - e^{0}}= \frac{0}{0}

You’ve got to be kidding me! No way we need to use L’Hôpital’s rule a third time, who would come up with this?????

Deeeeeeeep breathssssss….

Let’s give it one more go:

\frac{ \frac{d}{dz}(\pi^3 z) }{\frac{d}{dz}(1+ 4\pi z + 2\pi^2 z^2 - e^{-2\pi z})} = \frac{ \pi^3 }{4\pi + 4\pi^2 z +2\pi e^{-2\pi z}}

This seems promising, we can’t get zero in the numerator! Let’s plug in z=0 and hope for the best,

\frac{ \pi^3 }{4\pi + 0+2\pi e^{0}} = \frac{ \pi^3 }{4\pi +2\pi} \\ \\\textit{ }\qquad=\boxed{\frac{\pi^2}{6}}

WOW how amazing is this??????? It’s incredible! Our final result is,

\boxed{\textit{ }\textit{ }\sum_{n=1}^{\infty}\frac{1}{n^2} = \frac{\pi^2}{6}\textit{ }\textit{ }}

Who would have thought that summing square numbers would result in something with the circle constant \pi in there? Not me! I bet this was a kick in the discovery for Euler too!

Closing Remarks about Pi

Did you know it was Euler who standardized the use of the Greek letter \pi to represent 3.14159….? You might ask

“Why is \pi so special? Why does it deserve a holiday?”

Great questions! Of course, I don’t have the answers, but I would say that \pi is a surprising number. It shows up in the use of circles (not so surprising), it shows up in the sum of the reciprocals of the squares (very surprising), it shows up in the function for the probability density of the ground state in a quantum mechanical harmonic oscillator (which is used to describe light and very surprising), \pi is irrational (not so surprising), \pi is transcendental (maybe surprising?), it has weird looking infinite series like,

\frac{1}{\pi} = \frac{2\sqrt{2}}{9801} \sum_{n=0}^{\infty}\frac{(4n)!\;(1103+26390n)}{n^4\;(396^{4k})}

discovered by the great mathematician Srinivasa Ramanujan. And more and more! This is why it’s the spokes constant of math and why I think that it deserves a day of celebration.

Let me know in the comments your favorite places where \pi shows up unexpectedly!

For those who want even MORE pi, here are some of my favorite videos dedicated to pi in no particular order:

FUN \pi VIDEOS

*Sorry I couldn’t get the \pi to be larger*

Footnote:

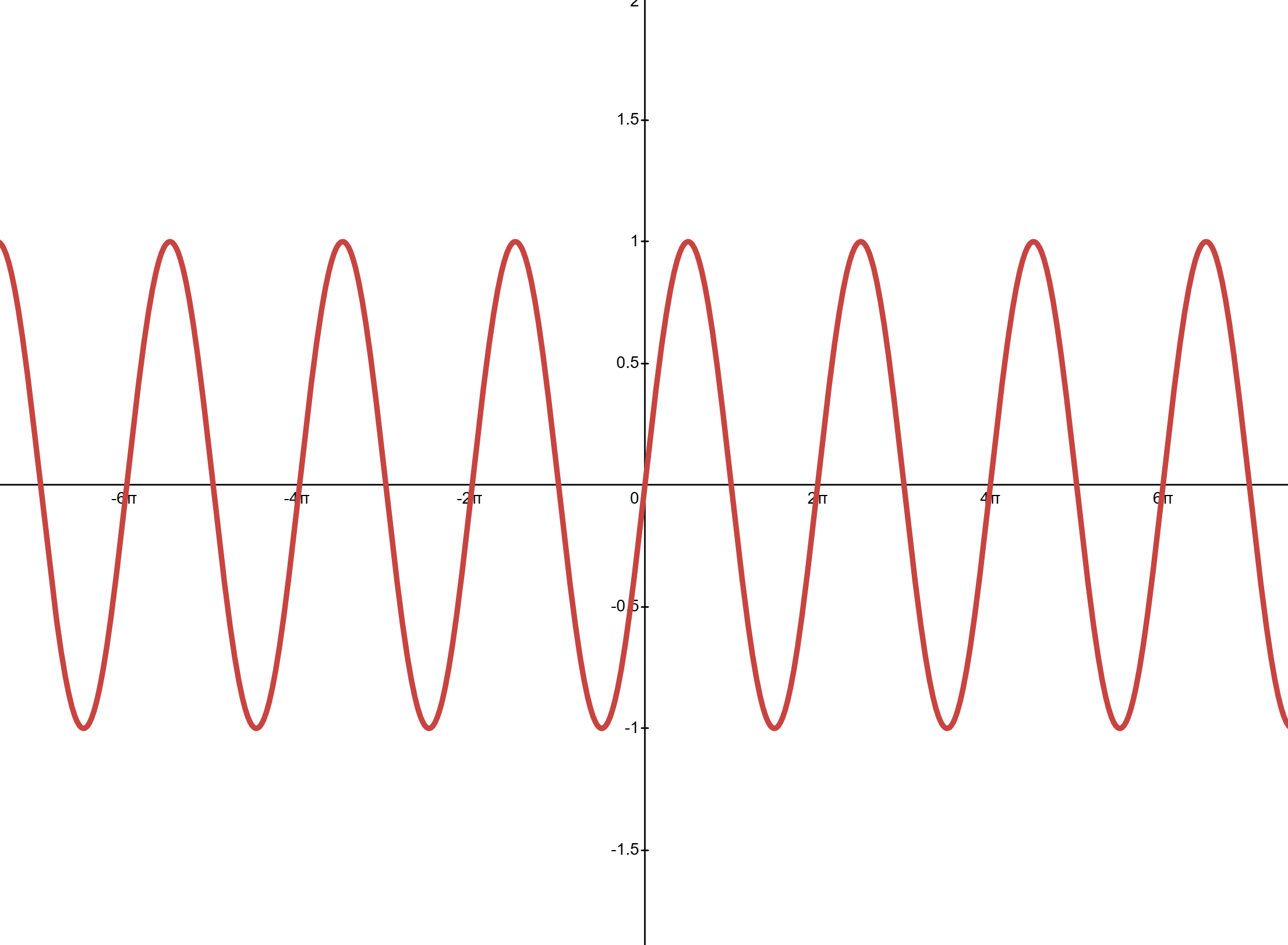
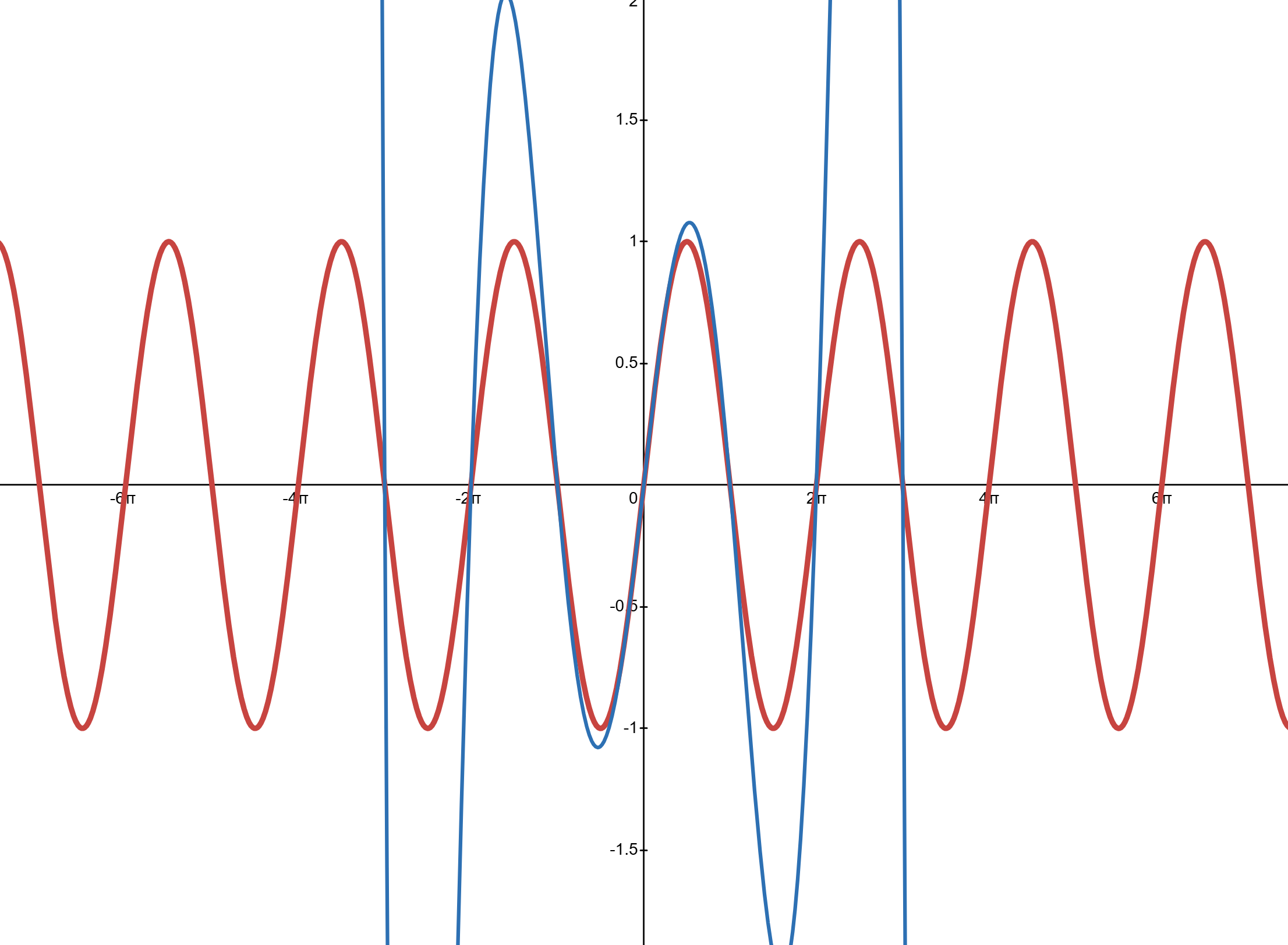
  1. Below is a series of graphs, the red is always \sin{x} and the blue is the functions are the following as you go along:
    Slide 2: Blue line is: x
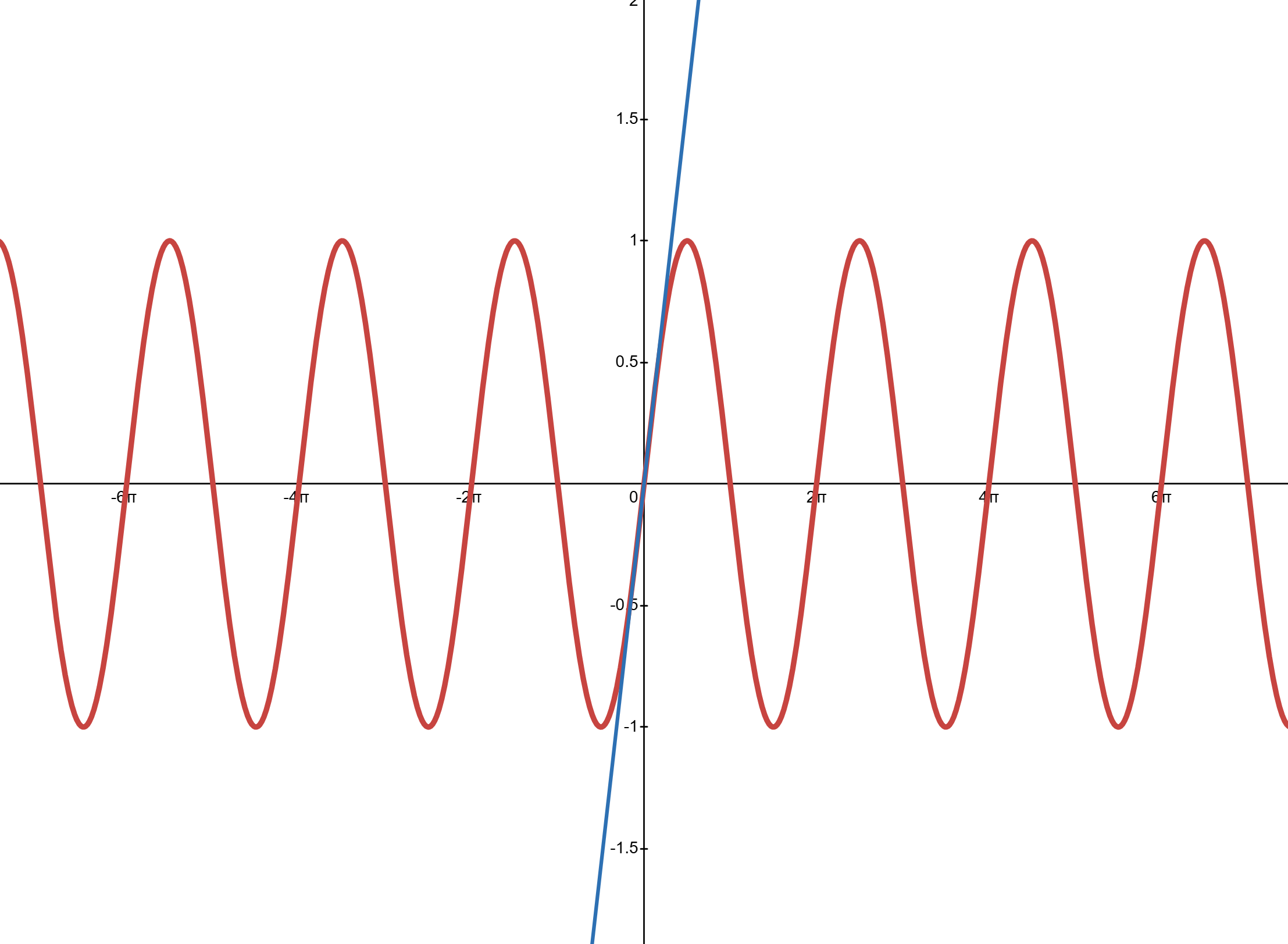
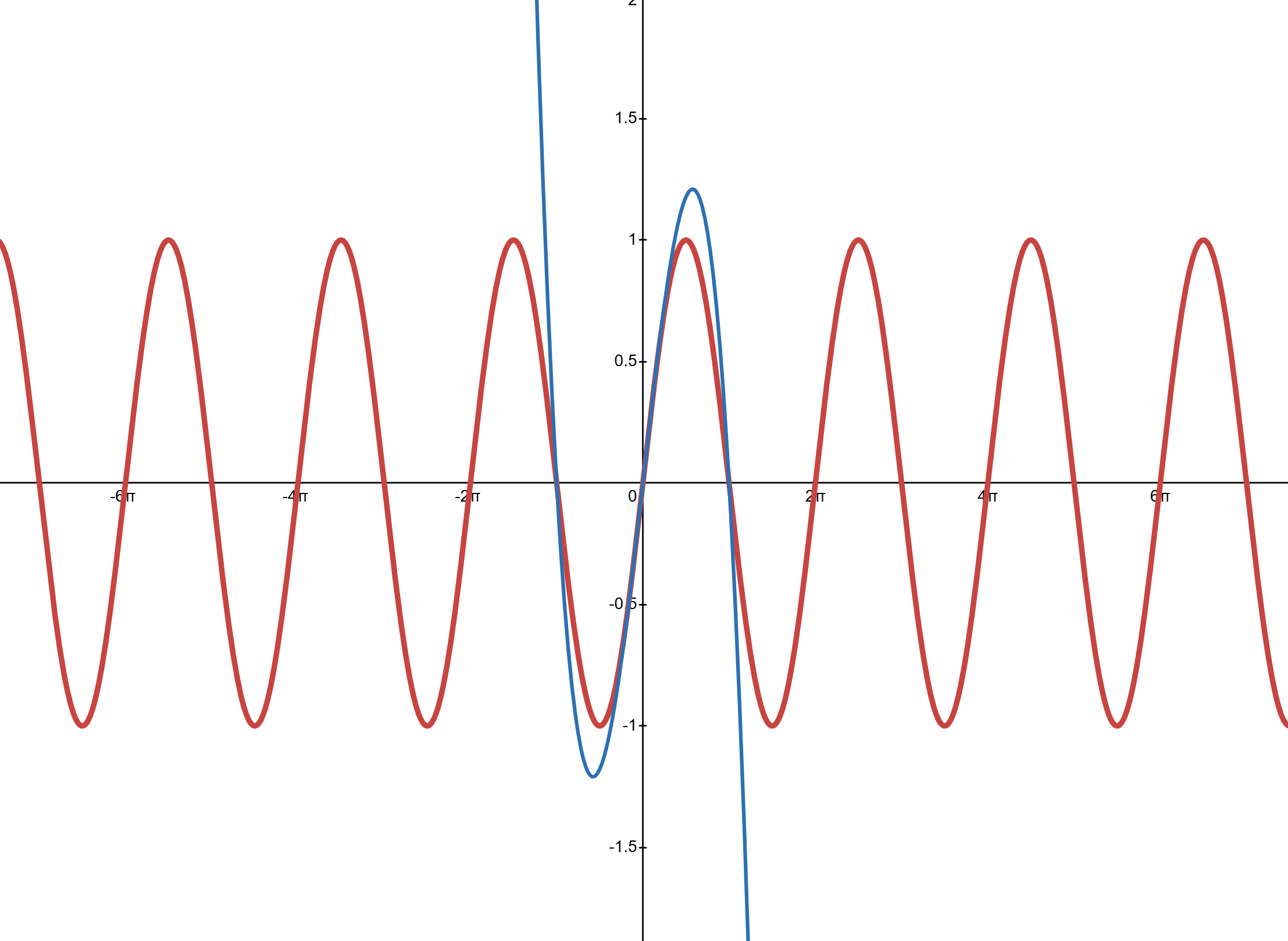
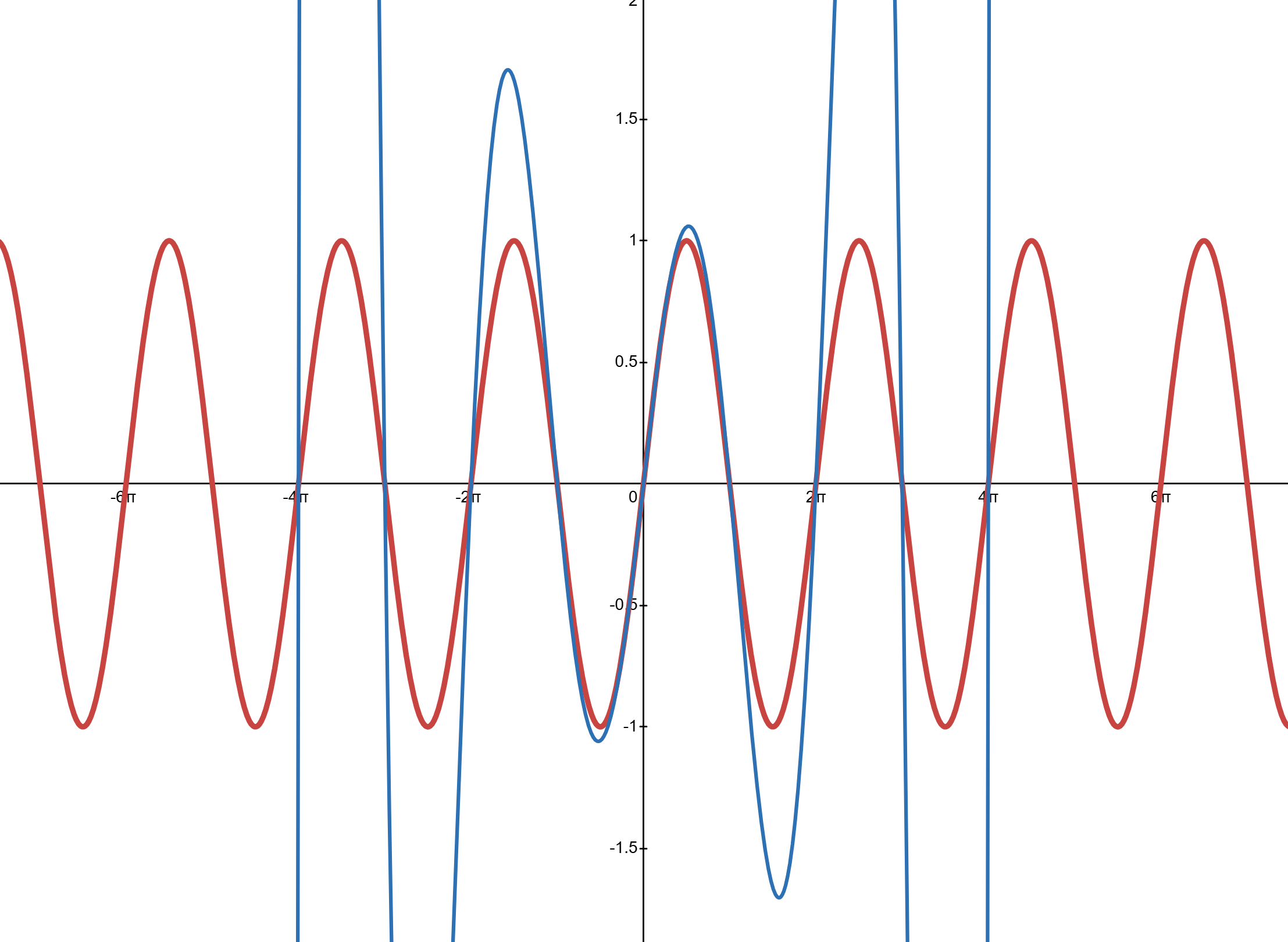
    Slide3: Blue line is: x \left( 1 - \frac{x}{\pi} \right)\left( 1 + \frac{x}{\pi} \right)
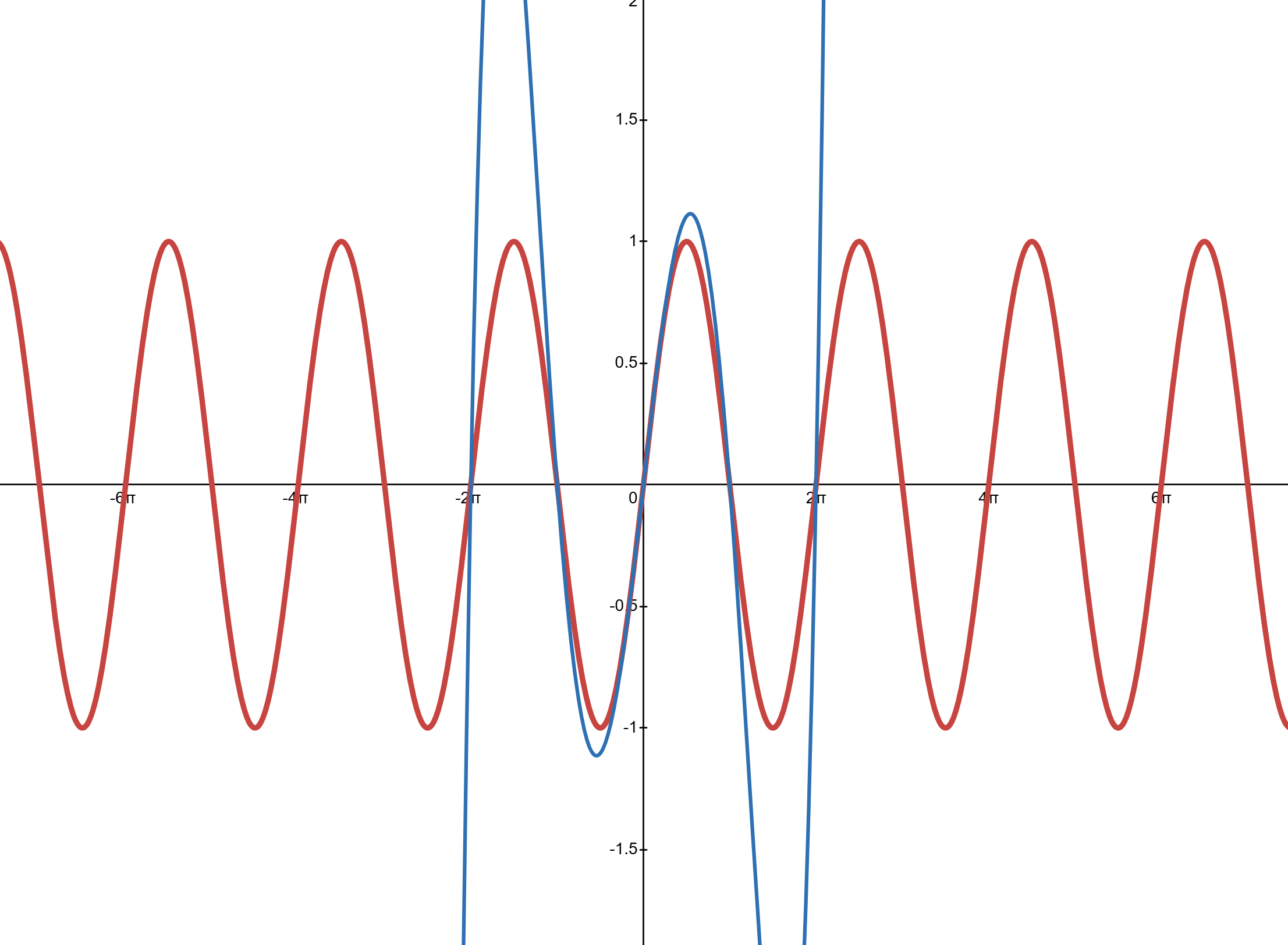
    Slide 4: Blue line is: x \left( 1 - \frac{x}{\pi} \right)\left( 1 + \frac{x}{\pi} \right)\left( 1 - \frac{x}{2\pi} \right)\left( 1 + \frac{x}{2\pi} \right)
    Slide 5: Blue line is: x \left( 1 - \frac{x}{\pi} \right)\left( 1 + \frac{x}{\pi} \right)\left( 1 - \frac{x}{2\pi} \right)\left( 1 + \frac{x}{2\pi} \right)\left( 1 - \frac{x}{3\pi} \right)\left( 1 + \frac{x}{3\pi} \right)
    Slide 6: Blue line is: x \left( 1 - \frac{x}{\pi} \right)\left( 1 + \frac{x}{\pi} \right)\left( 1 - \frac{x}{2\pi} \right)\left( 1 + \frac{x}{2\pi} \right)\cdots\left( 1 - \frac{x}{4\pi} \right)\left( 1 + \frac{x}{4\pi} \right)
    Slide 7: Blue line is: x \left( 1 - \frac{x}{\pi} \right)\left( 1 + \frac{x}{\pi} \right)\left( 1 - \frac{x}{2\pi} \right)\left( 1 + \frac{x}{2\pi} \right)\cdots\left( 1 - \frac{x}{5\pi} \right)\left( 1 + \frac{x}{5\pi} \right)
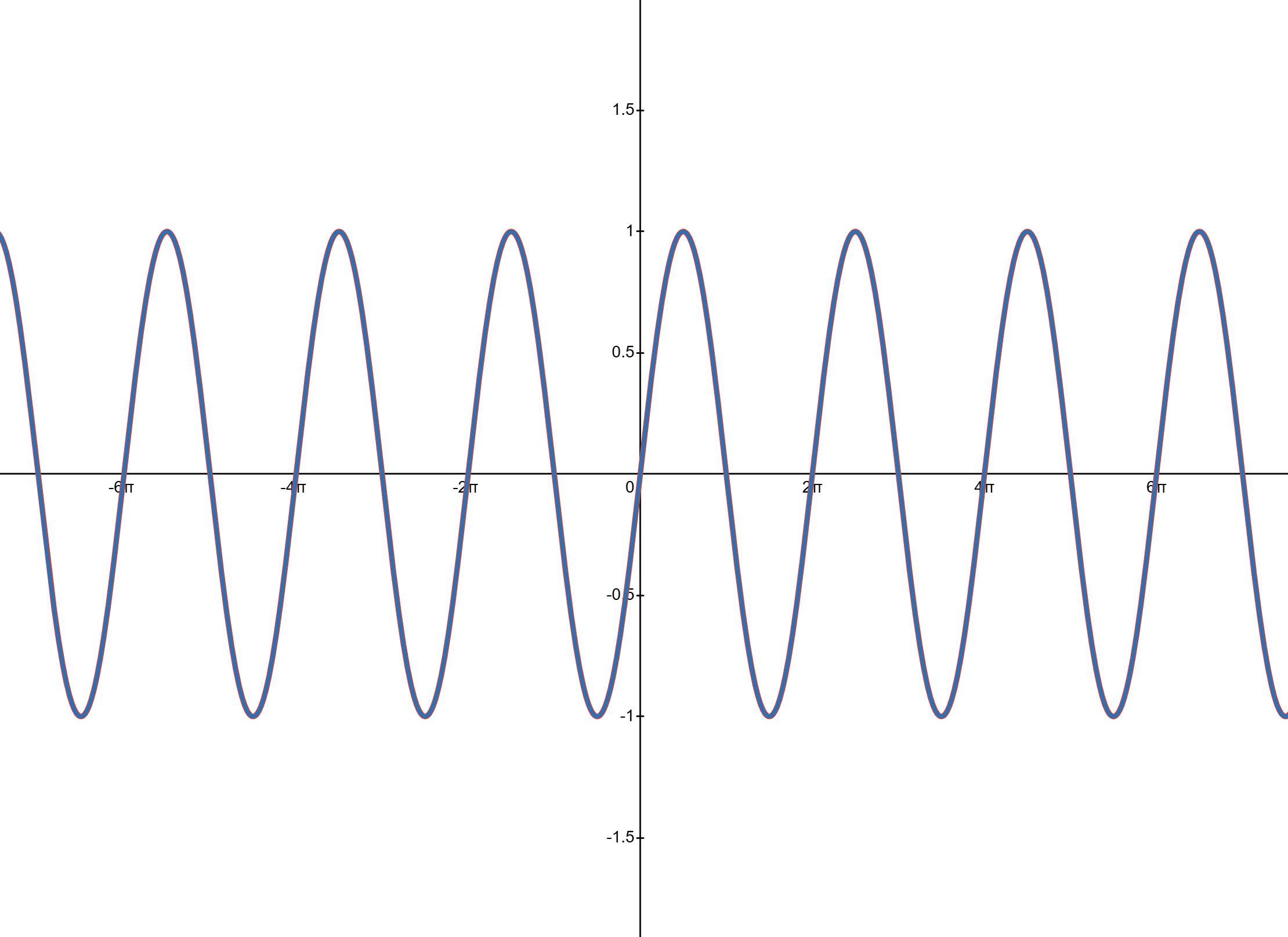
    Slide 8: Blue line is: x \left( 1 - \frac{x}{\pi} \right)\left( 1 + \frac{x}{\pi} \right)\left( 1 - \frac{x}{2\pi} \right)\left( 1 + \frac{x}{2\pi} \right)\cdots\left( 1 - \frac{x}{6\pi} \right)\left( 1 + \frac{x}{6\pi} \right)
    and then all the way up to 1,000,000.
    Slide 9: Blue line is: x \left( 1 - \frac{x}{\pi} \right)\left( 1 + \frac{x}{\pi} \right)\left( 1 - \frac{x}{2\pi} \right)\left( 1 + \frac{x}{2\pi} \right)\cdots \left( 1 - \frac{x}{1\;000\;000\pi} \right)\left( 1 + \frac{x}{1\;000\;000\pi} \right) ↩︎
  • This is just sin(x) graphed in red.
  • The equation x is graphed in blue.
  • Multiplied the zeros at pi and -pi to the previous blue line.
  • Multiplied the zeros at 2pi and -2pi to the previous blue line.
  • Multiplied the zeros at 3pi and -3pi to the previous blue line.
  • Multiplied the zeros at 4pi and -4pi to the previous blue line.
  • Multiplied the zeros at 5pi and -5pi to the previous blue line.
  • Multiplied the zeros at 6pi and -6pi to the previous blue line.
  • This is using all the zeros up 1,000,000pi and -1,000,000pi.

Leave a comment